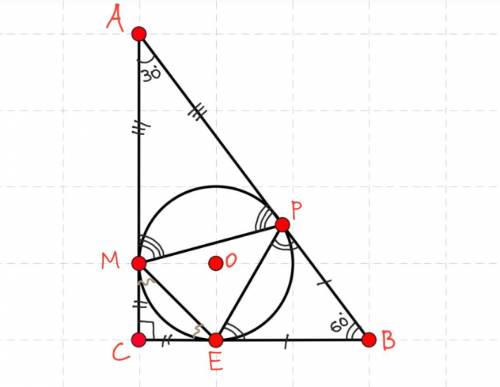
Дано: ΔABC — прямокутний (∠С=90°), ∠А=30°; коло, впис. у ΔABC; М, Р, Е — точки дотику,.
Знайти: ∠ЕМР, ∠МРЕ, ∠РЕМ.
Розв'язання.
Знайдемо третій кут прямокутного трикутника АВС. ∠В= 180°–∠С–∠А= 180°–90°–30°= 60°. (Сума кутів трикутника складає 180°)
1)Існує така властивість: відрізки, проведені з однієї вершини до точок дотику з колом, рівні.
Звідси, АМ=АР, РВ=ВЕ, ЕС=СМ. Це означає, що трикутники МАР, РВЕ і ЕСМ є рівнобедреними.
2) Розглянемо ΔМАР:
АМ=АР => ∠АМР=∠АРМ= (180°–∠А):2= (180°–30°):2= 150°:2= 75°.
3) У ΔРВЕ: ∠В= 60°, РВ=ВЕ => ∠ВРЕ=∠ВЕР= (180°–∠В):2= (180°–60°):2= 60°.
4) У ΔЕСМ: ∠С= 90°, ЕС=СМ => ∠СЕМ=∠СМЕ= (180°–90°):2= 90°:2= 45°.
5) Тепер ми можемо знайти всі кути трикутника МРЕ.
∠ЕМР= 180°–∠СМЕ–∠АМР= 180°–45°–75°= 60°.
∠МРЕ= 180°– ∠АРМ–∠ЕРВ= 180°–75°–60°= 45°.
∠РЕМ= 180°–∠ВЕР–∠СЕМ= 180°–60°–45°= 75°.
Відповідь: 45°, 60°, 75°.
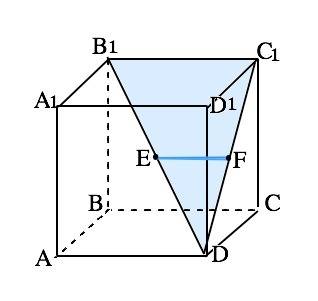
В ∆ В1DC1 отрезок EF соединяет середины сторон В1D и С1D, следовательно, EF- средняя линия и параллельна В1С1. Противоположные грани куба параллельны, противоположные стороны граней параллельны. ВС1 || А1D1, В1С1||ВС. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. ⇒ В1С1 параллельна плоскостям АBCD и ADD1A1.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо параллельна этой плоскости либо лежит в этой плоскости. EF параллельна В1С1,⇒ она параллельна АBCD и ADD1A1. EF параллельна В1С1, принадлежащей плоскости ВСС1В1 и А1В1С1D1, ⇒ прямая EF параллельна плоскостям четырех граней куба: АВСD. A1B1C1D1. AA1D1D, BB1C1C.
Відповідь:
Пояснення: фото