Задача для гениев. Есть две рейки (каждая из который длиной в 3 см), первая из них может свободно вращаться на 360 градусов, и к ней прикреплена вторая рейка, которая может вращаться тоже на 360 градусов относительно второй.Есть ли формула, чтобы вычислить угол обеих, чтобы край второй рейки, допустим, достиг точки (4, 5)
При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет , что больше 6.
Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно , и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и .
По теореме косинусов в треугольнике со сторонами a, b и c и углом справедливо соотношение . Для нашего треугольника данное выражение примет вид
Если достроим прямоугольный треугольник до прямоугольника так, чтобы гипотенуза была его диагональю (то есть присоединим к треугольнику второй такой же точно), то площадь такого прямоугольника будет ровно в 2 раза больше площади треугольника, то есть 2 * 512 * корень(3) = 1024*корень(3).
А также площадь прямоугольника равна произведению катетов. Обозначим меньший катет буквой х, тогда больший будет х*tg(x) = x*корень(3).
Итого, имеем площадь прямоугольника х*х*корень(3) = 1024*корень(3).
Корень(3) сокращаем, остаётся х*х = 1024. Отсюда х = корень(1024) = 32.
Пусть D, E и F - точки касания вписанной окружности со сторонами треугольника АВС: АС, АВ и ВС соответственно. Нам дано: АВ=30см, ВF=14см, FC=12см. Заметим, что ВЕ=ВF=14см, DC=FC=12см, а АЕ=АD как касательные, проведенные из одной точки к окружности. Тогда АЕ=АВ-ВЕ=30-14=16см, значит АD=16см. DC=FC=12см. Значит АС=AD+DC=16+12=28см. Полупериметр треугольника равен: р=(30+26+28):2=42см. Есть формула для вписанной в треугольник окружности: r=√[(p-a)(p-b)(p-c)/р], где р - полупериметр, а, b, c - стороны треугольника. В нашем случае: r=√(12*16*14/42)=√64=8см. ответ: r=8см. Или по формуле r=S/p, где S - площадь треугольника. Площадь найдем по формуле Герона: S=√[p(p-a)(p-b)(p-c)] или в нашем случае: S=√(42*12*16*14)=√(6*7*2*6*16*2*7)=6*7*2*4=336см². r=336/42=8см. ответ: r=8см.
Объяснение:
При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет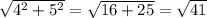 , что больше 6.
, что больше 6.
Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно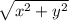 , и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и
, и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и 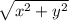 .
.
По теореме косинусов в треугольнике со сторонами a, b и c и углом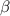 справедливо соотношение
справедливо соотношение 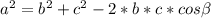 . Для нашего треугольника данное выражение примет вид
. Для нашего треугольника данное выражение примет вид 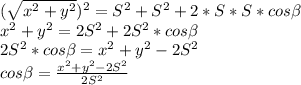
Отсюда искомый угол будет равен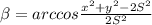 .
.