рассмотрим треугольник абе, параллелограмм абсд. так как сумма углов треугольника равна 180 градусов то угол абе равен 180-90(угол аеб)-60(угол бае) =30 градусов. в прямоугольном треугольнике катет напротив угла в 30 градусов равен половине гипотенузы, значит 2ае=ба, отсюдого следует что 2ае=ад - ад=ба. так как в параллелограмме противоположные стороны попарно равны, то ад=вс=ба=сд. значит все стороны этого параллелограмма равны, значит каждая сторона этого параллелограмма равна 36/4=9
теперь рассмотрим треугольник бсд. так как бс=сд, трегольник является равнобедренным или равносторонним. значит углы у основания бд равны.Также по свойству параллелограмма противоположные углы попарно равны, то есть угол бад равен углу бсд. сумма углов треугольника равна 180 градусов, значит угол сбд или сдб равны (180-60)/2=60 градусов. так как в этом треугольнике все углы равны 60 градусов треугольник - равносторонний, значит бд=вс=сд=9
ответ бд равен 9
Объяснение:
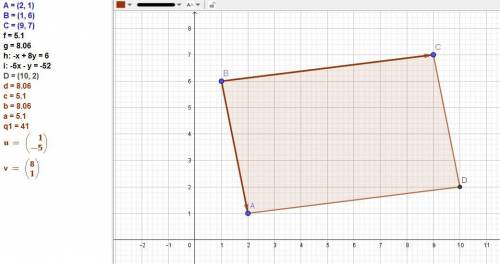
Площадь параллелограмма равна модулю векторного произведения векторов, выходящих из одной вершины.
Вектор ВА = (1; -5),
вектор ВС = (8; 1).
S = |a × b|
Найдем векторное произведение векторов:
c = a × b
a × b =
i j k
ax ay az
bx by bz
=
i j k
-1 5 0
8 1 0
= i (5·0 - 0·1) - j ((-1)·0 - 0·8) + k ((-1)·1 - 5·8) =
= i (0 - 0) - j (0 - 0) + k (-1 - 40) = {0; 0; -41}
Найдем модуль вектора:
|c| = √(cx² + cy² + cz²) = √(0² + 0² + (-41)²) = √(0 + 0 + 1681) = √1681 = 41.
Найдем площадь параллелограмма:
S = 41.
ответ: E=B
Объяснение: привет из оптимы;^