Объяснение:
1) Строю окружность с центром в т. О;
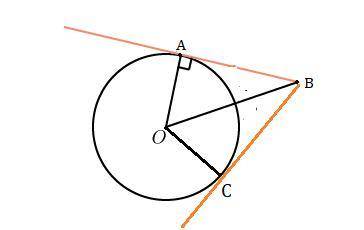
2) Беру т. В вне окружности , точку А на окружности, соединяем→ ВА- касательная ; из точки В провожу вторую касательную ВС.
3) Измеряю радиус ОА=3 см
Измеряю отрезки ВА и ВС ( это отрезки касательных) : ВА=4,1 см , ВС=4см. Примерно одинаковые⇒отрезки касательных проведенных из одной точки равны ( надо запомнить этот факт). Измеряю ВО=5,1 см.
Применяю т. Пифагора для ΔОАВ, ∠ВАО=90°.
ОВ²=5,1²=26,01≈26
ОА²+ВА²=3²+4,1²=9+16,81=25,81≈26 . Получили ОВ²=ОА²+ВА², т.е т. Пифагора выполняется .
Периметр квадрата вычисляется по формуле: Р = 4а, где а - сторона квадрата.
Значит, а = Р/4 = 6/4 = 3/2
Диаметр вписанной в квадрат окружности равен стороне этого квадрата => d = a = 3/2
Радиус окружности равен половине её диаметра
=> r = d/2 = (3/2) ÷ 2 = 3/4