Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
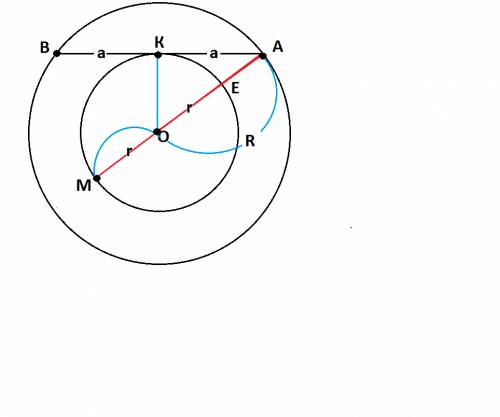
Для меньшей окружности точка А на большей окружности является внешней точкой.
АК²=АЕ*АМ
АЕ=R-r
AM=R+r
Пусть АК=а.
Тогда а²=(R-r)(R+r)=(R² -r²)
Т=π(R² -r²)⇒
Т=π*а²⇒
а=√(Т/π)
АВ=1а=2√(Т/π)
1) BC -?
2) (меньшая сторона) -?
1) AB/sin∠C =BC/sinA = AC/sin∠B = 2R (теорема синусов).
∠C =180° -(∠A +∠B )= 180° -(30° +105°) =45°.
16/sin45° =BC/sin30°⇒
BC =15*(sin30°/sin45°) =16*(1/2) / (1/√2) =(16√2)/2 =8√2≈11,28 (см).
---
2) меньшая сторона та, которая лежит против меньшего угла ,
эта сторона BC(лежит против меньшего угла ∠A=30°).
длину AC не требуется , но :
AC /sin∠B = AB/sin∠C ⇒AC =AB*sin(∠B)/(sin∠C)=
16* sin105°/(1/√2) =16√2sin105°=16√2*√2(√3 +1)/4 =8(√3 +1) .
sin105° =sin(180°-75°) =sin75°=sin(45°+30°) =...
или
sin105° =sin(60°+45°) =sin60°*cos45°+cos60°*sin45°=
(√3/2)*(√2/2)+(1/2)*(√2/2) =√2(√3 +1)/4.
* * * * * * * Второй
∠C =180° -(∠A+∠B) =180° -(30°+105°) =45°.
Проведем высоту BH⊥AC (∠AHB=90°) ⇒ Прямоугольный треугольник BHC равнобедренный CH =BH ,т.к. ∠C =45°.
По теореме Пифагора из ΔBHC:
BC =√ (BH² +CH²) =√(2BH²) =BH√2 . Но из ΔABH BH=AB/2 =8(как катет против угла
∠A =30°). Значит BC =BH√2 =8√2.