. За до малюнка 117 встановіть: а) чи паралельні прямі АВ і СD; б) міру кута KPM.

Question

Геометрия: . За до малюнка 117 встановіть: а) чи паралельні прямі АВ і СD; б) міру кута KPM.

tsukikokawaii · Accepted Answer

Основание - ромб ABCD. Вершина - M. О - пересечение диагоналей ромба.

Диагонали ромба взаимно перпендикулярны. Если одна диагональ 6, то её половина =3, а в прямоугольном треугольнике с катетом 3 и гипотенузой 5 второй катет равен 4, ну а вторая диагональ, следовательно, равна 8.

Т.е. пусть |AC|=6 => |AO|=|OC|=3; |BO|=|OD|=4; |BD|=8;

Из точки O опускаем перпендикуляр OE на сторону DC. Вычислим |OE|.

Можно из подобия треугольников OED и DCO, но проще и нагляднее через площадь, так как диагонали ромба взаимно перпендикулярны:

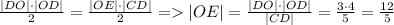
$\frac{|DO|\cdot|OD|}{2}=\frac{|OE|\cdot|CD|}{2} = |OE|=\frac{|DO|\cdot|OD|}{|CD|}=\frac{3\cdot4}{5}=\frac{12}{5}$

Ну, а высота ME, как гипотенуза OEM равняется:

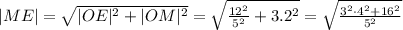
$|ME|=\sqrt{|OE|^2+|OM|^2}=\sqrt{\frac{12^2}{5^2}+3.2^2}=\sqrt{\frac{3^2\cdot 4^2+16^2}{5^2}}$

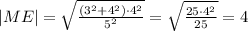
$|ME|=\sqrt{\frac{(3^2+4^2)\cdot4^2}{5^2}}=\sqrt{\frac{25\cdot4^2}{25}} = 4$

ответ: 4

MOGZ ответил