Question

Стороны египетского треугольника равны 3,4,5. Через центр вписанной в него окружности перпендикулярно гипотенузе провели прямую. Найдите длину отрезка этой прямой, заключённого внутри треугольника

Answer 1

$2\frac{1}{4}$ (ед.)

Объяснение:

Дано: ΔАВС - прямоугольный.

АС = 3; АВ = 4; ВС = 5.

Окр. O,r - вписанная.

ЕК ⊥ ВС.

Найти: ЕК.

1. Рассмотрим АМОР.

∠А = 90° (условие);

Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ОР ⊥ АС; ОМ ⊥ АВ.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ АМ || АР; АР || МО.

⇒ АМОР - прямоугольник.

Противоположные стороны прямоугольника равны.

⇒ АМ = АР; АР = МО.

МО = АР = r ⇒ АМ = АР = АР = МО.

⇒ АМОР  - квадрат.

2. Найдем r по формуле:

$\displaystyle r=\frac{a+b-c}{2}$ , где a и b - катеты, с - гипотенуза.

$\displaystyle r=\frac{3+4-5}{2}=1$

⇒ АМ = АР = АР = МО=1

3. Рассмотрим ΔАВС и ΔМВН - прямоугольные.

∠В - общий;

⇒ ΔАВС ~ ΔМВН (по двум углам).

Составим отношение сходственных сторон:

$\displaystyle \frac{BM}{AB}=\frac{MH}{AC}\\\\\frac{4-1}{4}=\frac{MH}{3}\\\\MH=\frac{3*3}{4}=\frac{9}{4}$

4. Рассмотрим ΔЕМО и ΔОКН - прямоугольные.

МО = ОК = r

∠1 = ∠2 (вертикальные)

⇒ ΔЕМО = ΔОКН (по катету и острому углу)

⇒ ЕО = ОН (как соответственные элементы)

МО +ОН = ЕО + ОК = МН =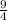 $\frac{9}{4}$

⇒

$\displaystyle EK=2\frac{1}{4}$