Маловато ...
Четырехугольник (не только трапецию) можно описать около окружности тогда и только тогда, когда суммы его противоположных сторон равны. В данном случае в трапеции сумма боковых сторон равна сумме его оснований. Следовательно полупериметром трапеции можно считать либо сумму боковых сторон, либо сумму оснований. В нашем случае нам нужна сумма оснований. Обозначим ее за р. Теперь есть формула для вписанной в четырехугольник (не только трапеция!) окружности
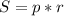
Здесь S - площадь трапеции, r - радиус вписанной окружности, р - полупериметр.
Остается только воспользоваться этой формулой
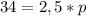
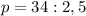
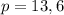
Как уже отмечали, полупериметр равен сумме оснований трапеции.
ответ: 13,6
![\frac{\sqrt[3]{x}*\sqrt[6]{x}}{\sqrt{x^3}}=\frac{x^{\frac{1}{3}}*x^{\frac{1}{6}}}{x^{\frac{3}{2}}}](/tpl/images/0154/9545/2fac9.png)
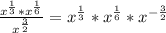
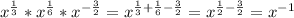
В случае, если х=0,2, то 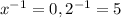
Решение:
Треугольник со сторонами 3,4,5 - прямоугольный (египетский).
Больший угол прямоугольного треугольника равен 90°.
Биссектриса делит сторону, к которой проведена, в отношении прилежащих сторон.
Следовательно, она делит гипотенузу в отношении 4:3, т.е. на 7 частей.
Пусть биссектриса равна х и разделила треугольник на два со сторонами в каждом:
4; 4*5/7 и х
3; 3*5/7 и х.
Для нахождения биссектрисы применим теорему косинусов.
Но манипуляции с косинусом 45°=(√2):2 нельзя назвать удобными.
Возьмем косинус одного из острых углов 3/5
Тогда стороны меньшего треугольника
3; 15/7 и х( биссектриса)
По теореме косинусов
х²=9+225/49-6*(15/7)*3/5
х²=288/49=144*2/49
х=(12/7 )*√2
Есть формулы, облегчающие нахождения биссектрисы, (если их знать и помнить).
Для биссектрисы из прямого угла это
L=√2(ab/(a+b)) где L- биссектриса, a и b - катеты.
По этой формуле
L=√2*3*4:(3+4)=√2*12/7
При желании можно вычислить, что это составит примерно калькулятору)