Тут через теоремку пифагорчика.
Мы знаем что это ПРЯМОУГОЛЬНАЯ трапеция, значит меньшая боковая сторона это высота, значит мы можем от конца меньшего основание провести еще одну высоту и мы получим прямоугольник треугольник
(найдем отрезок, который разделился при проведения высоты)
22-10=12 дм
Теперь мы знаем, что катеты равны 5 дм и 12 дм
Теорема Пифагора, с=sqrt(b^2+a^2) ( сори ,что написал в стиле информатики, sqrt - корень)
с=sqrt(25+144)
c=sqrt169
c= 13 дм
ответ: большая боковая сторона равна 13 дм
Точки X и Y лежат в плоскости α, а точка Z не находится в этой плоскости. Через серединные точки отрезков XZ и YZ проведена прямая b. Докажи, что эта прямая параллельна плоскости α.
(Дополни доказательство правильными словами или выражениями из списка.)
1. Если точки A и B — середины отрезков XZ и YZ, то отрезок AB
средняя линия треугольника
.
2. Как известно,
средняя линия треугольника
параллельна
третьей стороне треугольника.
3. Если прямая
параллельна
прямой, лежащей в некоторой плоскости, то она параллельна этой плоскости.
4. Значит, прямая b, на которой находится
средняя линия треугольника
,
параллельна
плоскости α, в которой лежит третья сторона треугольника.
Объяснение:
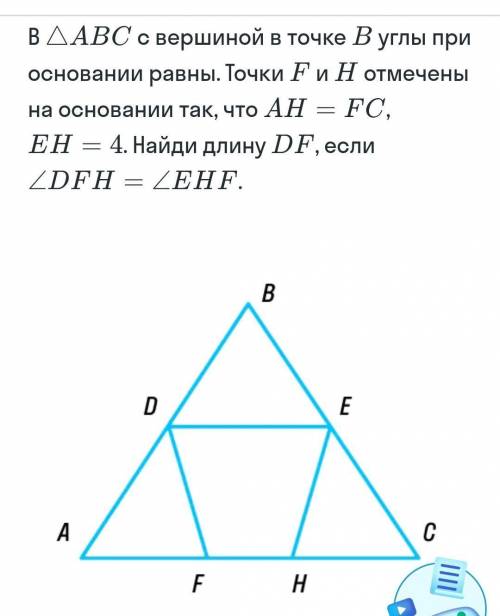
4 см
Объяснение:
1) AF = AH - FH
CH = FC - FH
Так как AH = FC по условию, то AF = CH.
2) ∠DFA = 180° - ∠DFH, так как эти углы смежные,
∠EHC = 180° - ∠EHF, так как эти углы смежные.
Так как ∠DFH = ∠EHF по условию, то ∠DFA = ∠EHC.
3) Рассмотрим ΔADF и ΔCEH:
AF = CH (доказано в п. 1)∠DFA = ∠EHC (доказано в п. 2)∠DAF = ∠ECH по условию, значитΔADF = ΔCEH по стороне и двум прилежащим к ней углам.
В равных треугольниках против равных углов лежат равные стороны:
DF = EH = 4 см