Объяснение:
52) ΔTMO=ΔQOM по стороне и двум прилеащим углам:
MO - их общая сторона, ∠TMO=∠QOM, ∠TOM=∠QMO (как сумма равных углов)
Как следствие, ΔTSO=ΔQSM, например, по стороне и двум углам:
QM=TO из равенства треугольников ΔTMO=ΔQOM, ∠QMS=TOS из условия, ∠QSM=TSO как вертикальные
53) Треугольники могут быть не равны - пример на рисунке. Так как заданы только равные углы, то стороны могут оказаться разными.
54) ΔABC=ΔEDC по стороне и двум прилежащим углам:
AC=CE по условию, ∠ACB=∠ECB как вертикальные углы, ∠BAC=∠DEC как смежные к равным углам.
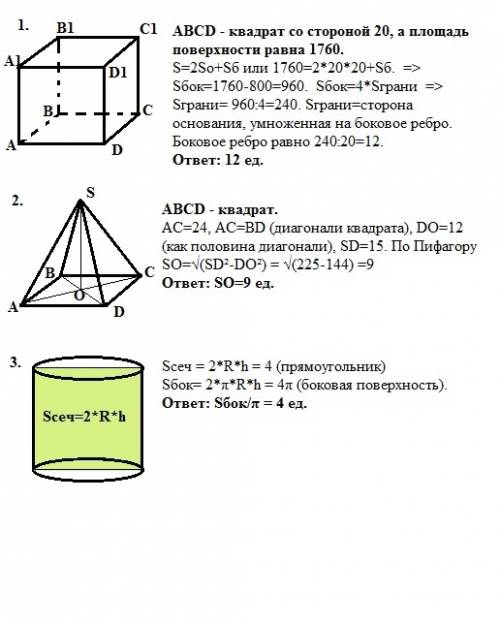
1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
ответ: Sбок/π = 4 ед.
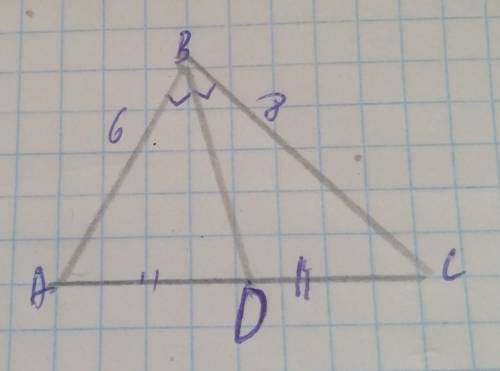
В•ab•BC=90•6•8=4320
Объяснение:
4320:90=48
ответ48
Кажетса так правильно