Для начала разберемся с углами;
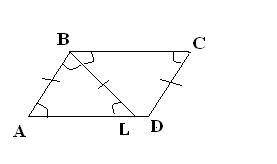
Из услвия дано, что угол BAL=BLA, следовательно, треугольник BAL равнобедренный и AB=BL=6, но т.к. ABCD-параллелограмм, то AB=CD=BL=6. Угол BAL=LBC как внутренние накрест лажащие при BC//AL и BL-секущая. Угол BAL=BCL, т.к. ABCD- параллелограмм. Т.к. BL-биссектриса, то угол ABL=LBC=BAL=60 градусов, т.е. треуголник ABL равносторонний. Значит AL=AB=6. Обозначим отрезок LD=x, тогда сторона AD=BC=6+x( т.к. ABCD-параллелограмм)
Запишем формулу периметра:
P=2(AB+AD)
24=2(6+6+x)
12=12+x
x=0
Значит точка L совпадает с точкой D. Тогда периметр LDCB будет равен периметру треугольника DBC
Перимитр ABC=6+6+6=18
из вершины В на АD опустим перпендикуляр, назовем его ВК. тогда, т.к. в треугольнике АВD стороны АВ и ВD равны получим, что ВК-медиана, биссектриса и высота в треугольнике АВD. значит ВК разделила АD пополам, то есть АК=КD=12/2=6.
по основному тригонометрическому тождеству находим cos А=корень из 1-sin квадрат А, то есть корень из 1-0,64=0,6.
из треугольника АВК соs А= АК/АВ, значит АВ=АК/cos A
АВ=6/0,6=10
по теореме Пифагора из треугольника АВК
ВК=корень из АВ квадрат минус АК квадрат
ВК=корень из 100-36= 8,
тогда площать параллелограмма АВСD=АD*ВК=12*8=96