ответ: 9 см и 23 см
Пусть трапеция АВСD, а ВК - биссектрисса тупого угла АВС. Поскольку она параллельна боковой стороне СD, то ВСDК - параллелограмм
Угол СDК равен углу АВК т.к. ВК - биссектриса.
Угол СDК равен углу КВС как противолежащие углы параллелограмма.
Угол СDК равен углу А, как углы при основании равнобокой трапеции. Следовательно, угол АВС равен двум углам А, и угол А + угол АВС =180° отсюда угол А = 60°, угол АВК = 60° и треугольник АВК - равносторонний АВ = АК = BK = 14, значит ВС + КD = 60 - (14*3) = 18. ВС = 18 : 2 = 9 см
АD = 9 + 14 = 23 см.
ответ: 10
Объяснение:
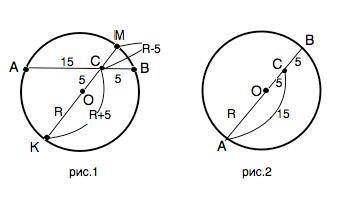
Сделаем рисунок 1 согласно условию задачи.
Проведем через О и С диаметр КМ, КО=ОМ=R.
КC=R+5, CM=R-5.
По т. о пересекающихся хордах ( а диаметр - наибольшая хорда окружности) при пересечении двух хорд окружности произведение отрезков одной хорды равно произведению отрезков другой хорды: АС•СВ=КС•СМ
15•5=(R+5)•(R-5) ⇒
R²-25=75
R²=100
R=10⇒
КМ=2R=20. Но АВ=АС+ВС=15+5=20. Следовательно, АВ - диаметр данной окружности, и рисунок должен выглядеть несколько иначе (см.рис.2. )