В окружность вписан квадрат со стороной 9 корней из 2 см. Найдите сторону правильного треугольника, описанного около этой окружности.
ответ:18√3 (см)
Объяснение:
Диаметром окружности, описанной около квадрата, является его диагональ. Точкой пересечения диагоналей квадрат делится на 4 равнобедренных прямоугольных треугольника, гипотенузы которых - стороны квадрата, а острые углы 45°. => r=9√2•sin45°=9
Центры окружностей, вписанных и описанных около правильного треугольника, совпадают ( это точка пересечения биссектрис, которые в то же время являются его срединными перпендикулярами).
Радиус вписанной в правильный треугольник окружности находят по формуле r=a:2√3 , где а - сторона правильного треугольника. =>
a=r•2√3
a=9•2√3=18√3 (см)
Угол С – угол между векторами АС и ВС.
1) Найдем координаты векторов АС и ВС.
Чтобы найти координаты вектора, нужно найти разность соответствующих координат точки конца вектора и начала.
Найдем координаты вектора АС:
АС (хс – ха; ус – уа);
АС (4 – 1; 5 – 1);
АС (3; 4).
Найдем координаты вектора ВС:
ВС (хС – хВ; уС – уВ);
ВС (4 – 4; 5 – 1);
ВС (0; 4).
2) Скалярное произведение векторов:
АС * ВС = 3 * 0 + 4 * 4 = 0 + 16 = 16.
3) Найдем длины векторов АС и ВС.
Квадрат длины вектора равен сумме квадратов его координат.
Найдем длину вектора АС:
|АС|2 = 32 + 42 = 9 + 16 = 25;
|АС| = 5.
Найдем длину вектора ВС:
|ВС|2 = 02 + 42 = 16;
|ВС| = 4.
4) Найдем косинус угла между векторами:
cos С = АС * ВС / (|АС| *|ВС|) = 16 / (5 * 4) = 4/5 = 0,8.
ответ: 0.8
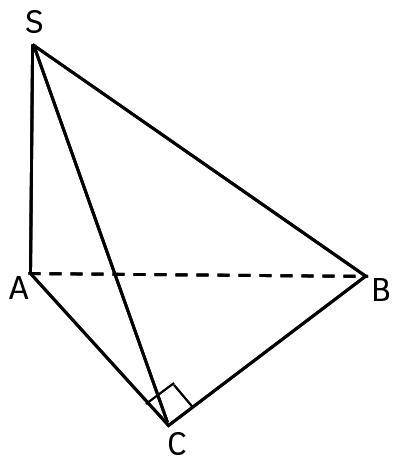
а)Так как SA⊥(ACB), где АС- проекция наклонной SC на плоскость ( АВС) , к тому же по условию АС⊥СВ, то по теореме о трех перпендикулярах SC⊥СВ, и, значит, ∠SCA-линейный угол двугранного угла между плоскостями ABC и SBC.
б) из прямоугольного треугольника SAB (∠SAB=90°) найдем
SA=√(SB²-AB²), АВ=√(7²+7²)=7√2; ⇒SA=√((7√5)²-(7√2)²)=7√3; из ΔSAC
tg∠SCA=SA/AC=7√3/7=√3⇒∠SCA=60°