
ответ: 11см
Объяснение:
ΔDHC-в нем гипотенуза 10см, один из катетов 8см, значит, другой катет √(10²-8²)=6 /см/; DH=6 см, а сторона АН состоит из двух отрезков АD=5см и DH=6 см, значит, АН=5+6=11/см/
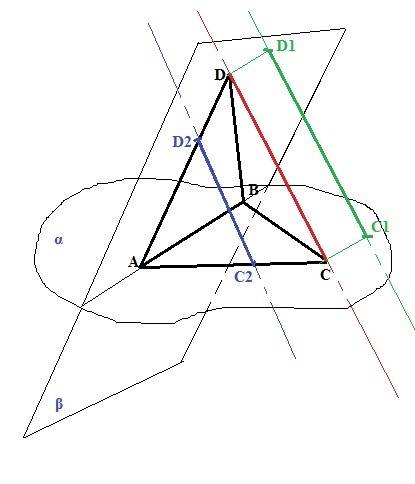
Есть теорема: "Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость". Отрезок CD имеет общую точку C с плоскостью АВС и общую точку D с плоскостью ABD. Через две точки можно провести только одну прямую, следовательно, прямая, содержащая отрезок СD, пересекает плоскость, содержащую треугольник АВС и плоскость, содержващую треугольник ABD. Значит любая прямая, параллельная СD, по приведенной теореме, также пересечет и плоскость АВС и плолскость ABD. Что и требовалось доказать.
11 см
Объяснение:
ΔСDН - прямоугольный, СD=10 см, СН=8 см, значит DН=6 см (египетский треугольник)
АН=AD+DH=5+6=11 cм