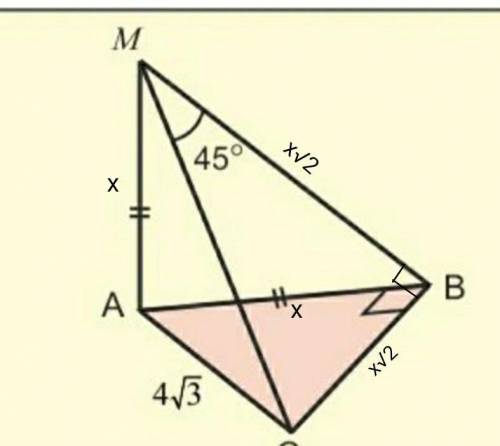
Пусть МА будет х, тогда АВ тоже будет х.
∆МАВ- прямоугольный равнобедренный треугольник.
МВ=√(МА²+АВ²)=√(х²+х²)=х√2
АВ⊥ВС, по условию
МВ⊥ВС, по Теореме о трех перпендикулярах.
∆МСВ- прямоугольный равнобедренный треугольник. Углы при основании равны. ∠СМВ=∠МСВ=45°
МВ=СВ=х√2.
∆АВС- прямоугольный треугольник
По Теореме Пифагора
АС²=АВ²+ВС²
Уравнение:
х²+(х√2)²=(4√3)²
х²+2х²=48
3х²=48
х²=48/3
х=√16
х=4 ед МА
∆МАС- прямоугольный треугольник
По теореме Пифагора
МС=√(МА²+АС²)=√(4²+(4√3)²)=
=√(16+48)=√64=8 ед.
ответ: МС=8ед.
Давай договоримся в дано ты пишешь все что тебе известно, здесь это прописывать очень долго и томно. Ладно?
Объяснение:
все что я объясняю щас пиши в решение, ниже будет шаблон оформления.
2. У треугольников АВС и ADC есть равные стороны AB=DC и AD=ВС и одна общая, значит у них все три стороны равны, и треугольники АВС и АDC подобны по 3 признаку равенства треугольников.
3. (похожая ситуация) у треугольников ОАВ и ОВС одна общая сторона и СВ=АВ, а ОА=ОС как радиусы окружности, значит треугольники ОАВ и ОВС равны по 3 признаку.
4.треугольники ВСN и МВС равны по 2 сторонам и углу, значит NB и МС делятся в точке о на одинаковые отрезки(NО=МО и ОВ=ОС)
если ОВ=ОС то треугольник равнобедренный
5. треугольники равны по условию, значит DB=AС и АС=11
Пример на примере 5 задачи
дано: ΔDAB; ΔCBA
в этом углу нарисуй чертеж DAB=CBA; САВ=DBА
из задания DB=11
Найти: АС-?
треугольники DAB и CBA равны по условию, значит DB=AС ⇒ АС=11
ответ: АС=11
PS: не знаю щас как у вас, лично нам в шк так учили оформлять.