Дано трикутники АВС і KLM. відомо що кут А 30°, кут С 65°, АС 4 см, кут М 65°, кут К 30°, КМ 4 см. чи рівні ці трикутники? а)рівні за кутом і стороною б)ні в)рівні за двома сторонами і кутом між ними г) рівні за стороною і двома прилеглими до неї кутами

👇

Увидеть ответ

Открыть все ответы

Ответ:

Niktommy

14.06.2022

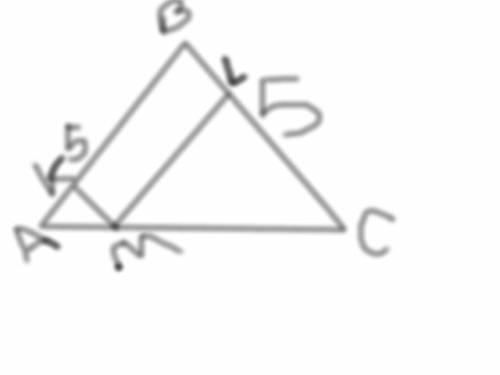
В прямоугольный ΔАВС, ∠С=90 вписан круг .Биссектриса ∠А делит катет в отношении CD:DB=3:5. Найдите площадь круга

Решение Площадь круга S= πr² .Радиус вписанной окружности найдем из формулы S=1/2*P*r .

1) Тк " биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника" , то CD:СА=ВD:АВ или 3:СА=5:АВ ⇒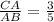 $\frac{CA}{AB} =\frac{3}{5}$ , а это по определению sinB .

2) По основному тригонометрическому тождеству

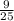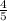
sin²B+cos²B=1 получаем cosB=√(1- $\frac{9}{25}$ )= $\frac{4}{5}$

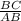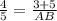3) cosB= $\frac{BC}{AB}$ или $\frac{4}{5} =\frac{3+5}{AB}$ ⇒ AB=10.

По т Пифагора АС=√(АВ²-ВС²)=√(100-64)=6

4) S=1/2*P*r

1/2*BC*AC=1/2*(AB+BC+AC)*r

1/2*8*6=1/2*24*r ⇒ r=2 ед

S(круга)=π*2²=4π (ед²)

4,4(6 оценок)

Ответ:

GorunovaSasha

14.06.2022

3) Три
Соединим все три вершины.
Получился треугольник, две стороны которого - стороны параллелограмма, и третья - его диагональ так как, убрав у любого параллелограмма вершину, и стороны, которые проходят через нее, получаем треугольник, состоящий из двух сторон и диаг. паралл.
Выбор расположения четвертой точки зависит от выбора стороны треуг., которая будет диагональю. Тогда возможны три варианта, так как у треуг. три стороны.
Чтобы построить паралл. при заданной диагонали, достаточно из концов диагонали построить прямые, параллельные сторонам, лежащим против соответствующих вершин. Точка их пересечения - четвертая вершина паралл.
2) Периметр равен 10
смотри рисунок - треуг AKM - равноб так как KM || BC => KM=AK;
ML = KB
Тогда ML + KM = AK + KB
ML+KM=5
P = 2(ML+KM)=10
3. сколько можно построить параллелограммов с вершинами в трёх заданных точках, не лежащих на одной