Геометрия: 5,7,8,если не тяжело можете с рисунком?

5,7,8,если не тяжело можете с рисунком?

👇

Увидеть ответ

Ответ:

DanilGorev

06.06.2023

5. 22см

7 номер не могу сделать, ибо нет рисунка.

8. CF=9см, <ABC=76°, <AFB=90°

Объяснение:

5. AB=BC=8см

треугABD=треугBCD по 2у признаку равенства треугольников(по двум углам и стороне)

=> AD=DC=3см

AC=3+3=6

Pabc=8+8+6=22см

7. AC=18см (по условию)

Т.к. AF=FC (т.к. BF — медиана), то CF=18:2=9см

Треугольник ABC равнобедренный (т.к. AB=BC), значит треугABF=треугBCD (по 1у признаку равенства треугольников, то бишь по двум сторонам и прилежащему к ним углу)

Значит <ABF=<FBC=38°

<ABC=<ABF+<FBC=38+38=76°

<ABC=76°

Т.к. Треуг ABC равнобедренный, то <A=<C, значит 180-76=104°

104:2=52°

<A=<C=52°

Далее берём треуг ABF. 180-38-52=90°

4,5(90 оценок)

Открыть все ответы

Ответ:

Kniga4001

06.06.2023

Объяснение:

№5

Вариант 1.

По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.

Исходя из этого:

АК=СК

ВК=DK

Так как

АВ=АК–ВК

СD=CK–KD

То:

АВ=СD.

Вариант 2.

Вариант 2.Проведём АС и BD.

По теореме: отрезки касательных, проведенные из одной точки к окружности, равны.

Тогда:

СК=АК

КВ=КD

Углы АКС и ВКD равны как вертикальные. Пусть каждый из них равен Y.

Рассмотрим треугольник АКС

СК=АК

Тогда треугольник равнобедренный с основанием АС.

Тогда угол АСК=(180–Y)÷2

Рассмотрим треугольник ВКD.

КВ=КD

Тогда треугольник равнобедренный с основанием BD

Тогда угол BDK=(180°–Y)÷2

Следовательно угол BDK=угол АСK.

Тогда АС||ВD, а углы BDC и АСD накрест-лежащие при параллельных прямых АС и ВD и секущей СD.

4,6(6 оценок)

Ответ:

Poli4ka228

06.06.2023

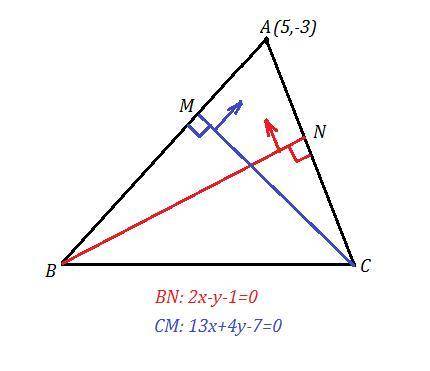
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

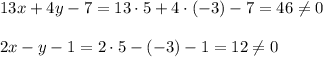
$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

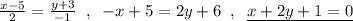
$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

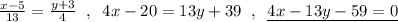
$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

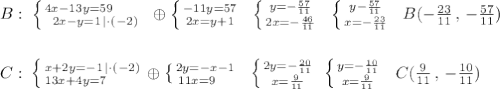
$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$