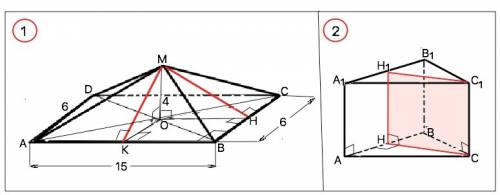
1. Основанием пирамиды служит прямоугольник со сторонами 6 и 15 см. Высота равна 4 см и проходит через точку пересечения диагоналей основания. Найти площадь боковой поверхности.
Пусть в пирамиде МАВСD AD=BC=6 см, AB=CD=15 см. По условию высота МО=4 см, О - точка пересечения диагоналей основания. Площадь боковой поверхности пирамиды равна сумме площадей боковых граней. Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому боковые грани - две пары равных равнобедренных треугольников. S (бок)=2•Ѕ(ВМС):2+2•Ѕ(АМВ):2. Высоты МК и МН боковых граней перпендикулярны сторонам основания, их проекции по т. о 3-х перпендикулярах перпендикулярны сторонам основания, параллельны соседним сторонам и равны их половине. ОК=СВ:2=3 см, ОН=АВ:2=8,5 см. Высоты боковых граней - гипотенузы прямоугольных треугольников МОК и МОН и по т.Пифагора МК= 5 см, МН=8,5 см. Ѕ(бок)=5•15+8,5•6=126 см²
—————————————
2. В правильной треугольной призме через боковое ребро перпендикулярно к противоположной боковой грани проведена плоскость. Вычислить полную площадь поверхности призмы, если площадь сечения равна 4,2√3, а сторона основания 6 см.
Площадь полной поверхности призмы равна сумме площадей двух оснований и площади боковой поверхности. По формуле площади правильного треугольника 2•Ѕ(осн)=2•6²•√3/4=18√3 см²
Площадь сечения - площадь прямоугольника со сторонами, равными высоте призмы и высоте основания. Высота основания ∆ АВС CH=AC•sin60°=3√3 см. Из площади сечения высота призмы СС1=4,2√3:3√3=1,4 см. Площадь боковой поверхности Ѕ(бок)=СС1•3•АС=1,4•18=25,2 см² =>
Ѕ(полн)=(18√3 +25,2) см²
Стороны правильного многоугольника равны.
Диаметр окружности, вписанной в квадрат со стороной m, равен длине его стороны.
d=m, r=d:2=m/2
Периметр квадрата=16 дм, => m=16:4=4 (дм) => r=4:2=2 (дм)
Длину стороны а правильного n-угольника, вписанного в окружность, находят по формуле
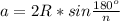
R=r=2 дм
n=5
180°:5=36°
sin36°= ≈0,5878
P=5a=10•2•0,5878= ≈11,7557 дм
Вариант решения:
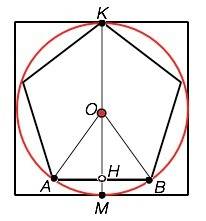
Рассмотрим рисунок приложения.
АВ- сторона пятиугольника., О - центр описанной окружности.
ОН - высота, медиана и биссектриса равнобедренного ∆ АОВ
Центральный угол АОВ вписанного пятиугольника 360°:5=72°
Угол АOН= 72°:2=36°
АН=ОА•sinАОН=2•sin36°, AB=2AH=4•sin36°
AB=4•0,5878 =≈2,35 (дм)
Периметр правильного пятиугольника со стороной а равен 5а
Р=5•АВ=≈11,7557 (дм)
45
Объяснение:
QWER - трапеция
QR=37
WE=21
S=1305
WH-высота
Найти : WH
S=(QR+WE) /2×WH
1305=(37+21)/2×WH
1305=29×WH
WH=1305:29
WH=45