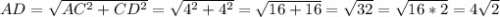
Так если один из углов при основании = 60 градусов, то второй угол при основании тоже равен 60 градусов (св-ва р.б. трапеции), вторая бокова сторона равно 8 см (опять же св-во р.б. трапеции)
проводим высоту вн из угла в (допустим трапеция авсд) , получаем прямоугольный треугольник, т.к. мы знаем два угла а=60градусов, и вна равен 90 градусов, то угол авн=30 градусов, значит ан равен 5 см, тк (в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы),если мы проведем из угла с высоту ск, то получим равный авн треугольник, следовательнокд равен 5 см, значит основание равно 8 + 10= 18
теперь периметр 8 + 18 + 10х2 = 46 см
проверьте на всякий случай, возможны опечатки , писала второпях :)
Объяснение:
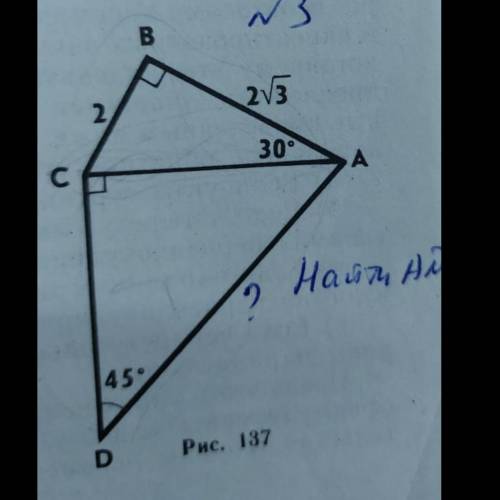
В прямоугольном треугольнике ABC против угла в 30° ( ∠CAB ) лежит катет ( BC = 2 ), равный половине гипотенузы ( AC ), поэтому AC = 2 * BC = 2 * 2 = 4.
В прямоугольном треугольнике ACD ∠CAD = 90° - 45° = 45°, следовательно треугольник ACD - равнобедренный, и AC = CD = 4. По теореме Пифагора