Ниже всё.
Объяснение:
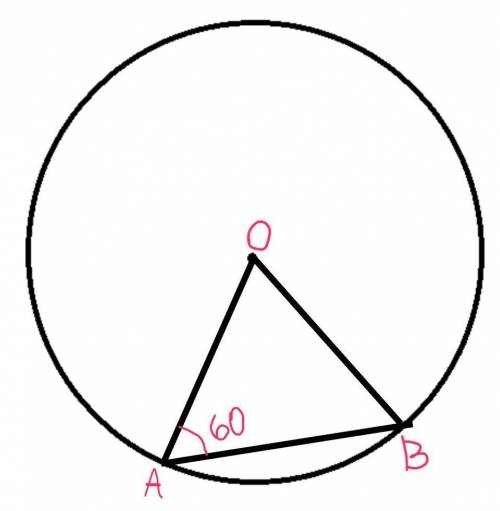
№1 (рисунок 1)
Дано:
ОВ и ОА – радиусы
АВ=6.
Угол ОАВ=60°
Радиусы всегда равны, тоесть АО=ВО.
Углы при основании равнобедренного треугольника равны, тогда угол ОВА=угол ОАВ=60°.
Сумма углов в любом треугольнике равна 180°, тогда угол АОВ=180°–угол ОВА–угол ОАВ=180°–60°–60°=60°.
Получим что ∆ОАВ – равносторонний, а значит ОА=АВ=6
ответ: 6
№2 (рисунок 2 и 3)
Для данной задачи есть два решения.
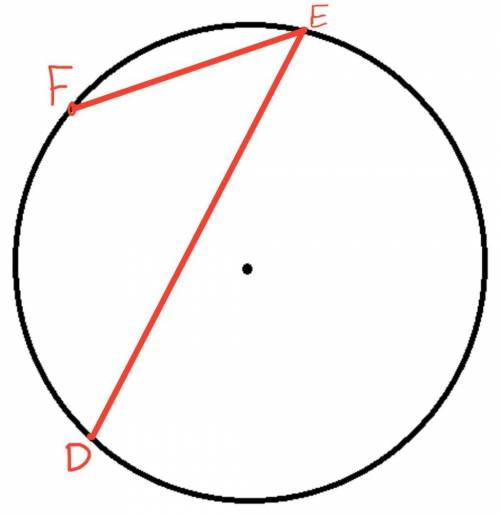
Для данной задачи есть два решения.1 Вариант (2 рисунок).
Если точка F лежит на дуге DE.
Дуга DF=дуга DE–дуга FE=150°–68°=82°
Угол DEF – вписанный и опирается на дугу DF, а следовательно, по теореме о вписанном угле, он вдвое меньше дуги DF.
Тогда угол DEF=82°÷2=41°.
ответ: 41°
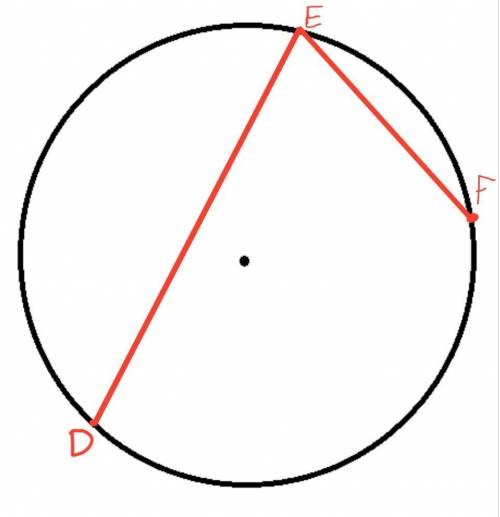
2 Вариант (3 рисунок).
Если точка F лежит вне дуги DE.
Дуга DF=360°–(дуга DE+дуга EF)=360°–(150°+68°)=360°–218°=142°
Угол DEF – вписанный и опирается на дугу DF. Тогда, по теореме об вписанном угле, он вдвое меньше дуги DF.
Тоесть угол DEF=142°÷2=71°.
ответ: 71°
Р =18 + 18 + 15,9 + 15,9 = 67,8 см
Объяснение:
Отрезки ОА и ОС - радиусы, проведённые из центра окружности к касательным ВА и ВС соответственно. ОА = ОС, как радиусы и равны 18 см из условия.
Радиусы, проведённые касательным окружности в точках касания А и С образуют углы 90°. Поэтому треугольники ΔОСВ и ΔОАВ - прямоугольные, углы АОВ и СОВ при точке O равны.
Поскольку треугольники ΔОСВ и ΔОАВ - прямоугольные, то неизвестная сторона при известных двух других может быть найдена по теореме Пифагора: c²=a²+b².
1) Найдём неизвестную сторону АВ треугольника ОАВ. Стороны ОА=18см - катет (а), ВО=24см - гипотенуза (с).
ВО² = ОА² + АВ², отсюда АВ² = ВО² - ОА²
АВ² = 24² - 18²
АВ² = 576 - 324 = 252 см²
АВ = √252= 15,9 см
2) Если у двух треугольников ΔОСВ и ΔОАВ равны:
стороны ОА = ОС - как радиусы, сторона ВО как общая, углы ∠АОВ = ∠СОВ, то треугольники равны по первому признаку равенства треугольников. А значит ВС=АВ=15,9 см.
3) Периметр четырехугольника АВСО равен:
АВ+ВС+ОС+ОА ,
Р =18 + 18 + 15,9 + 15,9 = 67,8 см