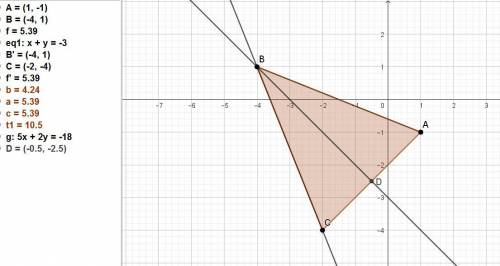
Даны A(1; -1), В(-4; 1) - вершины равнобедренного треугольника, х + у=-3 — биссектриса внутреннего угла между равными сторонами.
Найти уравнение стороны ВС.
Подставим координаты точки В в уравнение биссектрисы.
-4 + 1 = -3. Отсюда видно, что точка В - вершина треугольника при равных боковых сторонах.
Уравнение стороны ВС можно найти двумя путями.
1 - найти точку С как симметричную точке А относительно биссектрисы.
Потом составить уравнение ВС как прямую через 2 точки.
2- найти угол (точнее тангенс угла) между прямой АВ и биссектрисой. Затем определить угловой коэффициент стороны ВС по разности угловых коэффициентов АВ и биссектрисы (свойство симметрии прямых АВ и ВС относительно биссектрисы).
1) Находим к(AD) из уравнения биссектрисы у = -х - 3 .к(BAD) = -1
Уравнение AD: y =( -1/(-1))x + b.Подставим координаты точки A:
-1 =1*1 + b, отсюда b = -1 - 1 = -2. AD: y = x - 2 или х - у - 2 = 0.
Находим координаты точки D, решая систему уравнений BD и AD.
{х + у + 3 = 0
{x - y - 2 = 0
2x + 1 = 0 x = -1/2, y = x - 2 = (-1/2) - 2 = -2,5.
Находим координаты точки С как симметричной точке А относительно точки D.
x(С) = 2x(D) - x(A) = 2*(-1/2) - 1 = -2.
y(С) = 2y(D) - y(A) = 2*(-2,5) - (-1) = -4.
Теперь находим уравнение ВС. Вектор ВС = (-4-(-2); 1-(-4)) = (-2; 5).
(x + 4)/(-2) = (у - 1)/5.
Или в общем виде 5х + 2у + 18 = 0.
У тетраэдра все ребра равны. Так как по условию, точки М, К, Р середины отрезков АВ, ВД, ВС, то отрезок КМ средняя линия треугольника АВД, КР – средняя линия треугольника ВСД, МР – средняя линия треугольника АВС.
Отрезки средних линий параллельны основаниям треугольников: MK || АД, КР || СД, МР || АС, тогда и плоскость МКР параллельны плоскости АСД, что и требовалось доказать.
Длина средней линии треугольника равна половине длины параллельной стороны, тогда треугольник МКР подобен треугольнику АСД по трем пропорциональным сторонам с коэффициентом подобия К = АД / МК = АД / (АД / 2) = 2.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sавс / Sмкр = 48 / Sмкр = 22.
Sмкр = 48 / 4 = 12 см2.
ответ: Площадь треугольника МКР равна 12 см2.
Объяснение: правильно? ;-;