Апофема грани, высота пирамиды и расстояние от основания высоты до основания апофемы образуют прямоугольный треугольник. из него найдем половину стороны основания.
1/2 стороны основания= √(4а² - (а√2)²)=4а²-2а²=√2а² и равна а√2
а сторона основания равна 2а√2
Поскольку высота и половина основания равны в этом прямоугольном треугольнике, он - равнобедренный и угол между апофемой и средней линией квадрата в основании, что равносильно углу между боковой гранью и основанием,
равен 45 градусам.
Расстояние от центра основания пирамиды - перпендикуляр к апофеме. Поскольку угол между апофемой и плоскостью основания 45 градусов, получится равнобедренный прямоугольный треугольник с гипотенузой= половине стороны основания и катетами, равными половине апофемы = а.
Расстояние от центра основания до плоскости боковой грани =а
Площадь поверхности пирамиды равна сумме площади основания и площади боковой поверхности.
S основания =(2а√2)²=8а²
S боковая =4* 2а*а√2 =8а²√2
S полная =8а²√2+8а²=8а²(√2+1)
Чертёж смотрите во вложении.
Дано:
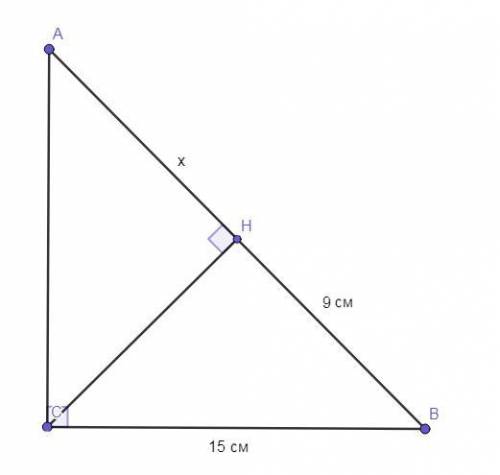
ΔABC - прямоугольный.
∠С = 90°.
СН - высота, проведённая к гипотенузе АВ.
НВ - проекция катета СВ на гипотенузу АВ = 9 см.
СВ = 15 см.
Найти:
S(ΔАВС) = ?
P(ΔАВС) = ?
Пусть АН = х.
По свойству проекций -
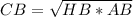
АB = 9 (cм)+х.
Подставим в формулу известные нам значения и решим полученное уравнение -
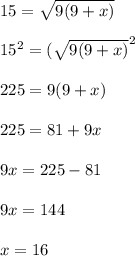
АН = х = 16 см.
АВ = 9 см+16 см = 25 см.
По теореме Пифагора -
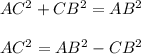
Подставим в формулу известные нам значения и найдём значение АС -
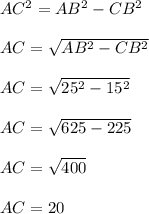
AC = 20 см.
P(ΔАВС) = АС+АВ+СВ = 20 см+25 см+15 см = 60 см.
Площадь прямоугольного треугольника равна половине произведения его катетов -
S(ΔABC) = 0,5*CB*AC
S(ΔABC) = 0,5*15 см*20 см
S(ΔABC) = 150 см².
ответ: 150 см², 60 см.
Объяснение:
Нехай основа х см, тоді бічні сторони по х+7 см.
х+х+7+х+7=37
3х=23
х=7 2/3
Основа 7 2/3 см, бічні сторони по 7 2/3+7=14 2/3 см