Все ребра правильной треугольной призмы АВСА1В1С1 равны между собой. Вычислите площадь сечения плоскостью, содержащей точку С и прямую А1В1, если площадь боковой поверхности треугольной пирамиды СС1АВ равна √3+4.
-----------
Поскольку призма правильная и все её ребра равны, то ее боковые грани - квадраты.
Сделаем рисунок.
S бок. пирамиды СС1АВ равно сумме площадей двух равных граней - равнобедренных прямоугольных треугольников АСС1и ВСС1 и наклонной грани- равнобедренного треугольника АС1В.
Пусть ребро призмы равно а.
S ACC1=S BCC1= а²:2
S AC1B=AB•C1H:2
АС1- диагональ квадрата и равна a√2
АН=ВН=а/2
Из ∆ АС1Н по т.Пифагора найдем С1Н.
С1Н²=АС1²-АН²=2а²-а²/4=7а²/4
С1Н=(a√7):2
S AC1B=a√7/2)•a/2=(a²√7):4
Sбок пирамиды=2•(а²:2)+a²√7/4= (4а²+а²√7):4=a²(4+√7):4
По условию a²(√7+4):4= √3+4
а² =4•(√3+4):(√7+4)
S A1CB1=S AC1B=(a²√7):4
Подставим значение а² в выражение S A1CB1=(a²√7):4
S A1CB1=[4•(√3+4):(√7+4)]•(√7):4
S A1CB1=√7•(√3+4):(√7+4) (ед. площади)

Объяснение:
1)
∆АВD- прямоугольный треугольник
По теореме Пифагора
ВD=√(AB²-AD²)=√(13²-12²)=√(169-144)=
=√25=5
BD=DC
BC=2*BD=2*5=10
ответ: ВD=10
2)
<RMK=180°- развернутый угол
<КМР=<RMK-<RMP=180°-135°=45°
<KMP=<MPK=45°
∆KMP- равнобедренный прямоугольный треугольник.
КМ=КР
КР=МР/√2=11/√2=5,5√2
ответ: х=5,5√2
3)
cos30°=KL/KR
cos30°=√3/2
√3/2=16/KR
KR=16*2/√3=32/√3=32√3/3
ответ: х=32√3/3
4)
Теорема Пифагора
МN=√(KM²+KN²)=√(12²+16²)=√(144+256)=
=√400=20
KT=KM*KN/MN
KT=12*16/20=9,6
ответ: х=9,6
5)
Теорема Пифагора
АС=√(АК²+КС²)=√(9²+12²)=√(81+144)√225=
=15
ВС=АС=15
ВК=ВС-КС=15-12=3
Теорема Пифагора
АВ=√(АК²+ВК²)=√(3²+9²)=√(9+81)=
=√90=3√10
ответ: х=3√10
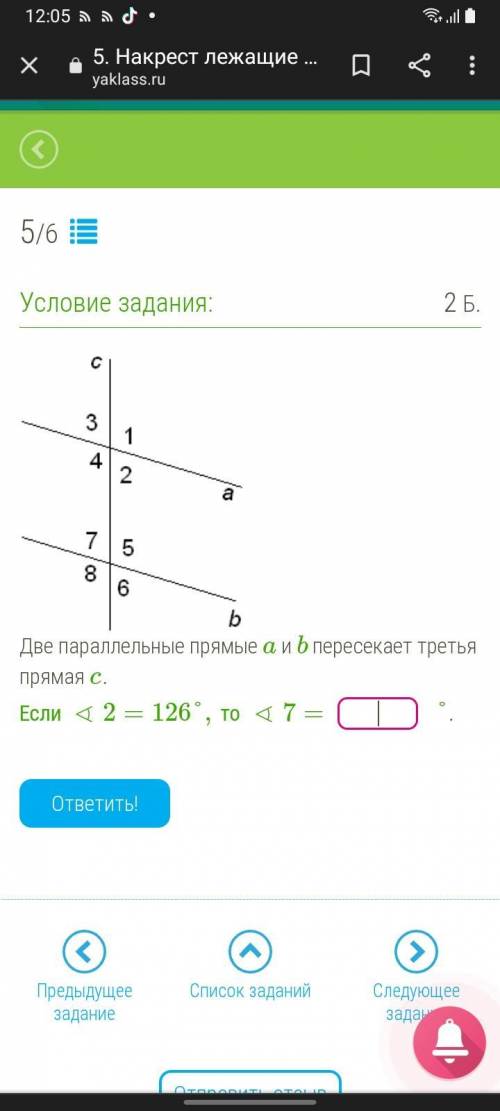
ответ:126
Объяснение:
2 и 3 углы вертикальные (они равны)
3 и 7 углы соответственные (тоже равны)
тогда 2 и 7 углы равны