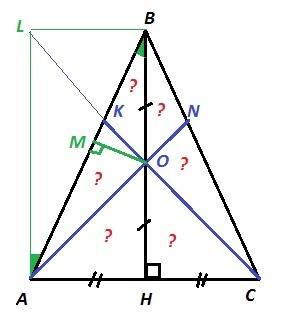
Дано: ΔABC : AB=BC; BH⊥AC; BO=OH
Найти: 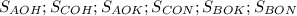
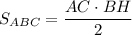
ΔABC - равнобедренный, высота BH является медианой и биссектрисой
⇒ AH = HC ⇒ ΔABH = ΔCBH - по двум катетам. Дальше можно рассматривать только одну половинку равнобедренного треугольника.
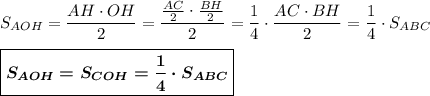
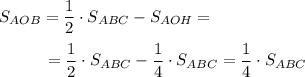
У треугольников AOK и BOK одинаковая высота OM. Поэтому их площади будут пропорциональны основаниям AK и KB. Чтобы найти отношение АК:КВ, достроим треугольник ABH до прямоугольника ALBH. LB=AH; AL=BH; LB║AH; AL║BH
∠AKL=∠OKB - вертикальные углы.
∠LAK=∠OBK - накрест лежащие углы при AL║BH и секущей АВ. ⇒
ΔAKL ~ ΔBKO подобны по двум углам:

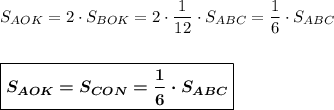
ответ: площади двух треугольников при основании равны и составляют 1/4 часть площади равнобедренного треугольника;
площади двух треугольников при вершине равны и составляют 1/12 часть площади равнобедренного треугольника;
площади двух треугольников при боковых сторонах равны и составляют 1/6 часть площади равнобедренного треугольника.
R=a²/√(4a²-b²), где a - боковая сторона треугольника, b - его основание.
Подставим известные значения: 16=a²/√(4a²-240). Пусть а²=Х.
Возведем обе части уравнения в квадрат:
256=Х²/(4Х-240). Имеем квадратное уравнение: Х²-1024Х+61440=0.
Отсюда Х=512±√(512²-61440)=512±√(512²-61440)=512±448.
Х1=960; Х2=64. Тогда а1=8√15; а2=8.
Но при боковой стороне треугольника равной 8 треугольник получается ТУПОУГОЛЬНЫМ. (По признаку существования треугольника: "если с - большая сторона и если a² + b² < c², то треугольник тупоугольный", а в нашем случае 64+64<240). Значит а=8 нас не удовлетворяет, так как не выдерживается условие, что треугольник ОСТРОУГОЛЬНЫЙ.
Центр описанной окружности треугольника лежит на пересечении серединных перпендикуляров к его сторонам. Тогда расстояние от центра до боковой стороны найдем из прямоугольного треугольника АНО, в котором гипотенуза - радиус описанной окружности, а катет - половина боковой стороны.
OH=√[R²-(a/2)²]=√(256-240)=4.
ответ: расстояние от центра окружности до боковой стороны равно 4.