Завдання 2-го етапу Всеукраїнської олімпіади юних математиків 2021 р. 7 клас 0. Яке з чисел є розв'язком рівняння 3y – 4 = 1 А. 5/3 Б. 4/3 в. 1 Г. 3/5 1. Миколка і Петрик задумали по цілому числу. Миколка знайшов їхню різницю, i а Петрик їхній добуток. Потім вони разом вирахували добуток отриманих чисел. Чи могли вони одержати число 20202021? 2. Представте число 100°у вигляді суми чотирьох доданків, які задовольняли б наступним умовам: якщо від першого доданка відняти 4, до другого додати 4, третій помножити на 4, а четвертий розділити на 4, то завжди вийде одне і те ж число. 3. Знайдіть площу прямокутника, складеного з квад- ратів (див. рис.), якщо його периметр 34 см. 4. На дошці записані числа 3, 6, 9, 12. Дозволяється з суми будь-яких двох з них, відняти третє і записати нове число на дошці. Чи можна через якусь кількість таких операцій отримати число 2021? (Відповідь обгрунтуйте). 5. Три понеділка місяця припали на парні числа. Яким днем тижня було 19 число цього місяця?
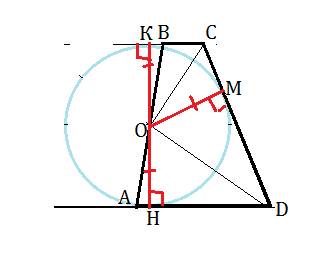
1. Т.к. ∠OGA=∠OFA=∠OHA=90°, то все точки A,G,O,F,H лежат на одной окружности с диаметром AO.
2. Треугольник ABC подобен треугольнику HFG т.к. ∠GAF=∠GHF и ∠FGH=∠FAH=∠BCA по свойству вписанных углов.
3. L - центр окружности вписанной в HFG, т.к.:
a) ∠OHF=∠OHG (опираются на равные хорды),
б)∠GFL=∠OFL-∠OFG=(90°-∠FOL/2)-∠OFG=(90°-∠FAH/2)-∠OAG, ∠GFH=180°-2∠OAG-∠FAH, т.е. ∠GFL=∠GFH/2.
Из а) и б) следует, что L - точка пересечения биссектрис треугольника HFG.
4. Из 2 и 3 следует, что в треугольнике ABC отрезку AO соответствует отрезок HL, т.е. коэффициент подобия ABC относительно HFG равен AO/HL=AO/(OH-OL)=25/(13-7)=25/6. Отсюда BC=GF*25/6.
5. Из прямоугольного треугольника AOF получаем NF/OF=AF/AO, т.е. GF=2NF=2OF·AF/AO=(14√(25²-7²))/25=336/25. Тогда из 4 видим, что
BC=(336/25)·(25/6)=56.
6. Высота параллелограмма ABCD равна EO+OH=7+13=20. Значит, площадь равна 20·BC=20*56=1120.
P.S. Есть ощущение, что BC можно и проще найти, но... :))