дана трапеция abcd где ad большее основание. на стороне ad отмечена точка H такая что AH=8 HD=7 BH=15 боковая сторона трапеции равна 17. докажите что треугольник abh прямоугольный и вычислите площадь трапеции
Угол ВМО - линейный угол двугранного угла, образованного плоскостью треугольника с данной плоскостью α. ВМ и МN перпендикулярны АС, значит плоскость ANC (плоскость α) перпендикулярна плоскости BMN. Углы между наклонными (две другие стороны треугольника) и плоскостью - это углы между этими наклонными и их проекциями на эту плоскость. Перпендикуляр ВО к плоскости α лежит в плоскости BMN (О на прямой MN). Надо найти синусы углов ВСО и ВАО. Прямоугольные треугольники ВАО и ВСО равны по гипотенузе и катету. Углы ВСО и ВАО равны. Из прямоугольного треугольника ВМО : , sinВСО = sin ВАО = ответ
, 
60
Объяснение:
треугольник ABH прямоугольный т.к. по теореме пифогора: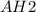
+ BH2 =
= AB2; 64 + 225 = 289 = 17 2(в квадрате) ⇒ BH - высота к AD ⇒ Sabcd =
7 ⇒ Sabcd = 1/2 * 15 * 8 = 60