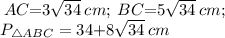
Объяснение:
Дано:
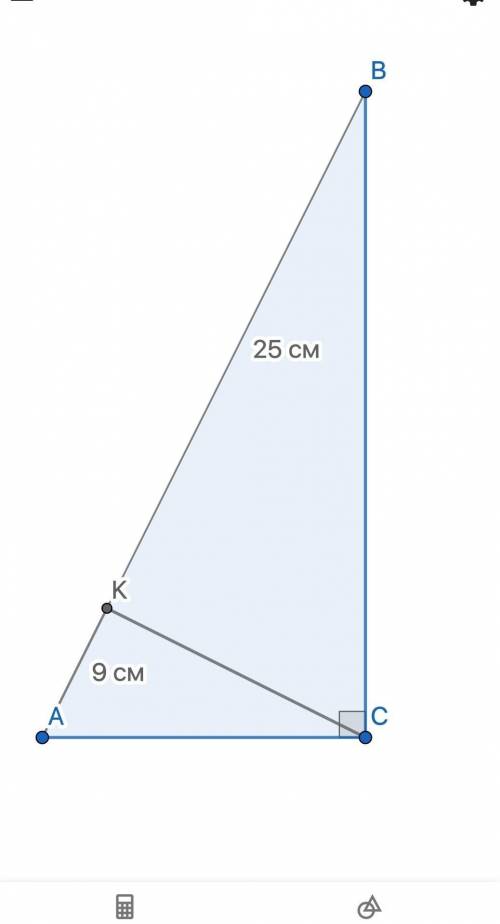
∆АВС, уг.С = 90°
СК _|_ АВ; АК = 9 см; ВК = 25 см
Найти:
АС, ВС, Р(∆АВС) - ?
т.к. в ∆АВС угол С прямой, то:
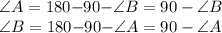
Рассмотрим ∆АСК и ∆ВСК:
т.к. СК _|_ АВ, =>
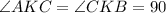
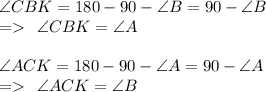
Следовательно ∆АСК и ∆СВК - подобны,
и соответственно:
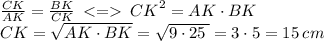
Далее по Т. Пифагора найдем стороны АС и ВС:
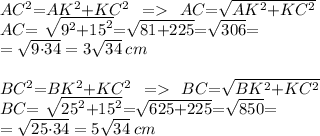
А длина стороны АВ равна сумме длин ее частей:
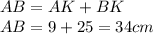
Найдем периметр ∆АВС:
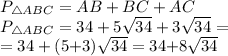
Итак:
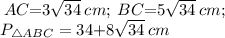
Проверим квадраты сторон треугольника АВС:
AB=5, BC=12, AC=13.
5² +12² = 25 + 144 = 169,
13² = 169. Треугольник АВС - прямоугольный, угол АВС - прямой.
Поэтому треугольник АМС лежит в вертикальной плоскости.
Проверим квадраты сторон треугольника ВМС:
ВМ=15, BC=12, МC=9.
9² +12² = 81 + 144 = 225,
15² = 225. Треугольник ВМС - прямоугольный, угол ВМС - прямой.
Угол α между плоскостями треугольника ABC и прямоугольника ABMN соответствует плоскому углу МВС.
α = arc sin(MC/BM) = arc sin(9/15) = arc sin(3/5) = 0,643501 радиан = 36,8699°.
Дано:
ΔABC - прямоугольный и равнобедренный
∠С = 90° AC = BC
AB = 12 см CM⊥(ABC)
CM = 6 см
--------------------------------------------------------------------
Найти:
ρ(M,AB) - ?
1) На рисунке проведем CH⊥AB
2) CM⊥AB, так как CM⊥(ABC), AB⊂(ABC)
CH⊥AB по построению, значит, MH⊥AB по теореме о трёх перпендикулярах, тогда MH = ρ(M,AB)
3) Так как ΔABC - прямоугольный и равнобедренный, то CH - высота и медиана, тогда:
CH = AH = BH = 1/2 × AB = 1/2 × 12 см = 6 см
4) CM⊥(ABC), CH⊂(ABC), значит, CM⊥CH и ΔMCH - прямоугольный.
5) Воспользуемся по теореме Пифагора в ΔMCH:
MH² = CM² + CH² - теорема Пифагора
MH = √CM² + CH² = √(6 см)² + (6 см)² = √36 см² + 36 см² = √72 см² = √36×2 см² = 6√2 см ⇒ ρ(M,AB) = MH = 6√2 см
ответ: ρ(M,AB) = 6√2 см
P.S. Рисунок показан внизу↓
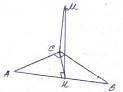
В прямоугольном треугольнике высота, проведенная к гипотенузе, есть среднее геометрическое между отрезками гипотенузы⇒
h=√(9*25)=3*5=15(см)
ΔАСК , т Пифагора АС=√(15²+9²)=√306 см
ΔВСК, т Пифагора ВС=√(15²+25²)=√850см
Р=(9+25)+√306+√850=34+3√34+5√34=34+8√34