1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)
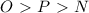- всё это конечно углы.
АС=16см
<А=60°
<В=60°
<С=60°
Объяснение:
∆ABC- равнобедренный треугольник, по условию. АВ=ВС=16см
В равнобедренном треугольнике высота ВD- является также медианой.
АD=DC
∆ABD- прямоугольный треугольник
По теореме Пифагора
АD=√(АВ²-ВD²)=√(16²-(8√3)²)=
=√(256-192)=√64=8см.
АC=2*AD=2*8=16см
АС=АВ=ВС, треугольник ∆АВС- равносторонний.
В равностороннем треугольнике все углы по 60°