
Угол АОС=120° Меньшая дуга АC=120°,
большая дуга АC=360°-120°=240°
Возможны два случая расположения т.В.
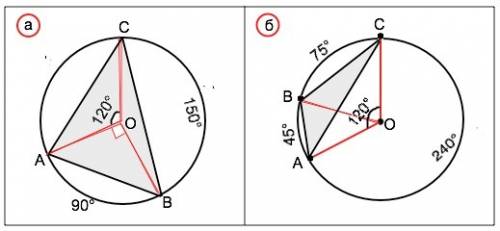
а) Точка В расположена на большей дуге АС.
Точка В делит дугу 240° в отношении АВ=3 части, ВС=5 частей. ⇒
◡АВ=240°:8•3=90°; ◡ВС=240:8•5=150°.
Тогда в ∆ АВС его вписанные углы равны:
угол В равен половине центрального угла АОС=120°:2=60°.
Угол С равен половине центрального АОВ и равен 90°:2=45°.
Угол А=половине центрального СОВ и равен 150:2=75°⇒
Углы ∆ АВС равны 45°, 60°, 75°
б) Точка В расположена на меньшей дуге АС.
◡АВ=120°:8•3=45°; ◡ВС=120°:8•5=75°
Вписанные углы равны половине градусной меры дуг, на которые опираются.
∠А=75°:2=37,5°
∠С=45°:2=22,5°
∠В=240°:2=120°
Углы ∆ АВС равны 22,5°; 37,5°; 120°.
ответ: ∠1>∠2,
Объяснение:
против меньшей стороны лежит меньший угол, угол 1 равен углу РТQ, как вертикальный ему, помимо этого, он еще и внешний при вершине Т, поэтому равен ∠Р+∠Q, т.е. равен сумме углов, с ним не смежных, получается, что ∠1 больше как угла Р, так и углу Q, ( угол 2 вертикален углу Q, значит, ему равен), получается,
∠1>∠2, т.е. доказано без участия сторон)