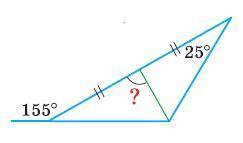
ответ: 90°
Объяснение:
180 - 155 = 25
Если два противоположных угла одинаковы (то есть 25 и 25) то треугольник равнобедренный. Значит проведенная высота также является биссектрисой.
25 + 25 = 50
180 - 50 = 130
130 : 2 = 65
Находим углы мелкого треугольника.
65 + 25 = 90
180 - 90 = 90.
Неизвестный угол равен 90°.
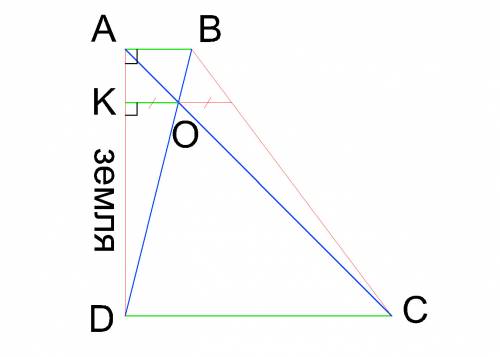
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м

90° потому что зеленая полосочка медиана