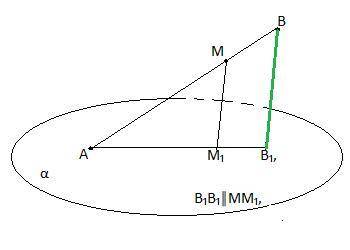
Точка A - конец отрезка AB лежит в плоскости. Через конец отрезка точку B и точку M, принадлежащую отрезку AB, проведены параллельные прямые, пересекающую данную плоскость в точку B₁, M₁ соответственно. Найдите длину отрезка BB₁, если MM₁ = 9см, AM = 4см, MB = 6см
Объяснение:
ΔВАВ₁ подобен ΔМАМ₁ по по двум углам :
∠А-общий, ∠АММ₁ =∠АВВ₁ как соответственные при B₁В₁║МM₁, АВ-секущая. Кстати, АВ=4+6=10 (см)
В подобных треугольниках сходственные стороны пропорциональны : АВ:АМ= ВB₁:МM₁ или 10:4=ВB₁:9 или ВB₁=(10*9):4,
ВB₁=22,5 см
Уравнение параболы y^2=4x выразим через у: y = ±2√x, что соответствует двум ветвям параболы выше и ниже оси Ох.
Пусть абсцисса точки касания хо.
Общее уравнение касательной: y = y(xo) + (y'(xo))(x - xo).
Производные равны: y' = ±(1/xo).
Подставляем данные для верхней ветки, получаем:
y = 2√xo + (1/√xo)*(x - xo) = (2xo + x - xo)/√xo = (xo + x)/√xo.
Так как прямая проходит через точку М(-1, (8/3)), то:
(8/3) = (xo - 1)/√xo.
Возведём обе части уравнения в квадрат.
(64/9) = (xo² - 2xo + 1)/xo.
9xo² - 18xo + 9 = 64xo. Получаем квадратное уравнение:
9xo² - 82xo + 9 = 0.
D=(-82)^2-4*9*9=6724-4*9*9=6724-36*9=6724-324=6400;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root6400-(-82))/(2*9)=(80-(-82))/(2*9)=(80+82)/(2*9)=162/(2*9)=162/18=9;
x_2=(-2root6400-(-82))/(2*9)=(-80-(-82))/(2*9)=(-80+82)/(2*9)=2/(2*9)=2/18=1/9~~0.111111111111111.
Имеем 2 абсциссы точек касания, значит, касательных будет две.
Вторая точка соответствует нижней ветви параболы, так как уравнение касательной одинаковое.
Координаты точек касания B(9; 6), A((1/9); (-2/3)).
Уравнения касательных имеют вид:
y(B) = (1/3)x + 3,
y(A) = -3x - (1/3).