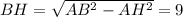Дано:
треугольник ABC: ac = 26, ab = 6√3, ∠a = 60°.
Найти:
S - ?
1) Из точки B проведем высоту BD на сторону AC.
Рассмотрим треугольник ABD:
Так как ∠A = 60°∠BDA = 90°, ∠B = 30°, значит катет, лежащий против угла в 30 градусов равен половине гипотенузы.
АD = 3√3.
2)Найдем длину BD. По теор. Пифагора:
BD² = AB² - AD²;
BD² = (6√3)² - (3√3)² = 36×3 - 9×3 = 108 - 27 =81 .
BD = 9.
3) Найдем площадь:
S= 1/2ah = 1/2×AC×BD.
S = 1/2 × 26 × 9 = 117.
ответ: S = 117.
AC:16=7:3––АС=16•7:3=28 см
Объяснение:
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
AC:16=7:3––АС=16•7:3=28 см
ответ: 117
Объяснение:
Обозначим вершины треугольник как показано на рисунке
Проведем высоту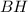
Тогда,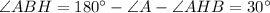
По теореме Пифагора