Вычислите площадь трапеции abcd с основаниями ad и bc, если а= 24 см, вс= 16 см, угол а = 45, угол d = 90

👇

Увидеть ответ

Ответ:

James0123

07.04.2023

Дано:

трап. ABCD

AD и BC основания

AD=24 см

BC=16 см

угол D=90

угол A=45

Найти:

S(abcd)-?

Проведем высоту BH.

Так как трап. прямоугольная то AH=AD-BC=24-16=8 см

Рассм. тр. ABH - по усл. угол A=45, угол H = 90 - BH высота, то угол B = 45, отюда тр. равнобедренный, а занчит AH=BH=8 см

S=1/2*(a+b)*h

S=1/2*(16+24)*8=1/2*40*8=20*8=160 см²

ответ. площадь трапеции равна 160 см²

4,8(81 оценок)

Открыть все ответы

Ответ:

Genius2020

07.04.2023

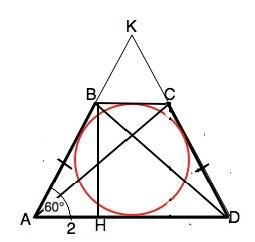
Обозначим вершины трапеции АВСD, АВ=СD, АD - ВС=4.

Опустим высоту ВН. Высота равнобедренной трапеции, опущенная из тупого угла, делит большее основание на отрезки, меньший из которых равен полуразности, больший - полусумме оснований.

АН=4:2=2.

ВН=АН•tg60°=2√3

ВН - диаметр вписанной окружности. r=√3.

Продолжив боковые стороны трапеции до их пересечения в точке К, получим равносторонний ∆ АКD с вписанной в него окружностью. Формула радиуса вписанной в правильный треугольник окржуности

r=a√3):6,

√3=a√3:6, откуда а=6. АD=АК=DК=6

НD=6-АН=4

Диагонали равнобедренной трапеции равны. АС=BD

ВD•BD=BD²

BD²=BH²+HD²=(2√3)²+4²=28

Вравнобедренную трапецию с острым углом 60, одно из оснований которой на 4 больше другого, вписана о

4,4(73 оценок)

Ответ:

karinakazakova5

07.04.2023

Билет № 2
3. В окружность вписан треугольник ABC так, что АВ - диаметр окружности. Найдите углы треугольника, если: а) ВС=134°
АВ - диаметр - > < C=90 < A=67 (вписанный угол) < B=180-90-67=23

Билет № 3
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника.
Так как четырехугольник описан вокруг окружности, то сумма других сторон равна 12
S=p*r=(a+b+c+d)*r/2=24*5/2=60

Билет № 4
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Дан треугольник ABC. AB=BC. M - точка касания вписанной окружности стороны АВ. N - точка касания вписанной окружности стороны ВC. K - точка касания вписанной окружности стороны АC. AM=3. MB=4.
В соответствии со свойством касательных, проведенных из одной точки к окружности
AM=AK CK=CN BM=BN
P=3+3+4+4+3+3=20

$\sqrt[n]{x}$