Рассмотрим 2 треугольника ABC- остроугольный и EFG- . тупоугольный, в котрых провели высоты CD и EH. - id2103540020230328 от ирпимрпмро 28.03.2023 00:02

Question

Геометрия: Рассмотрим 2 треугольника ABC- остроугольный и EFG- . тупоугольный, в котрых провели высоты CD и EH. Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне. Sabc= 1/2 ABCD Sefg= 1/2 FG* EH Выведем формулу для вычисления площади каждого из данных треугольников. треугольник ADC-, CD=; треугольник EHG-, ЕН= Sabc= 1/2 АВ Sefg= 1/2 FG Что вставить в пропуски: EG sin G, AC sin A, EG cos G, AC cos A, прямоугольный, остроугольный, прямоугольный, тупоугольный, AC sin

ирпимрпмро · Accepted Answer

Дано6
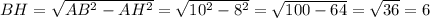
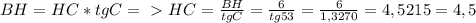
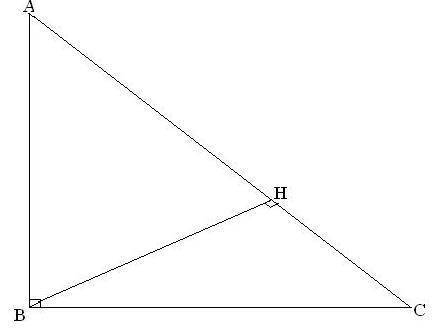
Треугольник АВС- прямоугольный (угол В=90градусов), ВН - высота, АН=8, АВ=10
Найти: АС

Решение:
АС=АН+НС
1)Рассмотрим треугольник АВН, он прямоугольный, по определению высоты
$BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6$
Катет противолежащий углы=равен произведению гипотенузы на синус этого угла, то есть
$BH=AB*sinBAC=\ \textgreater \ sinBAC=\frac{BH}{AB}=\frac{6}{10}=0,6$
Используя таблицу Брадиса найдем значение угла и получим, что угол ВАС=37 градусов
2) Рассматриваем треугольника АВС
угол АСВ=180-угол ВАС-угол СВА=180-37-90=53градуса
3)рассмотрим треугольник ВНС
Катет противолежащий углу равен произведению другого катета на тангенс этого угла, то есть
$BH=HC*tgC=\ \textgreater \ HC=\frac{BH}{tgC}=\frac{6}{tg53}=\frac{6}{1,3270}=4,5215=4,5$
4)AC=AH+HC=8+4,5=12,5
ответ: АС=12,5

Точка н является основанием высоты проведенной из вершины прямого угла в треугольника авс к гипотену

Точка н является основанием высоты проведенной из вершины прямого угла в треугольника авс к гипотену

MOGZ ответил