
Угол между меньшей диагональю и большей боковой
стороной раваен 90°.
Объяснение:
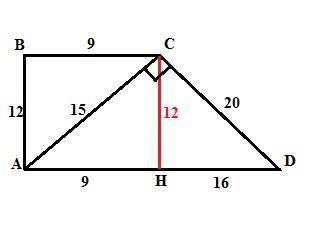
Пусть дана прямоугольная трапеция АВСD с прямыми углами А и В. В прямоугольном треугольнике АВС катет АВ по Пифагору равен
АВ = √(АС²-ВС²) = √(15²-9²) = 12 ед. Опустим высоту СН.
СН = АВ = 12 (противоположные стороны прямоугольника).
Тогда в прямоугольном треугольнике HCD по Пифагору:
НD = √(CD²-CH²) = √(20²-12²) = 16 ед.
AD = AH+HD = 9+16 = 25 ед.
В треугольнике АСD стороны равны:
АС=15ед, CD = 20ед, (дано), a AD = 25 ед (найдено выше).
Следовательно, треугольник АСD - прямоугольный с прямым углом ACD, так как выполняется условие AD² = AC²+CD² (проще говоря, треугольник Пифагоров с соотношением сторон 3:4:5).
ответ: угол между меньшей диагональю и большей боковой
стороной равен 90°.
По-моему так.
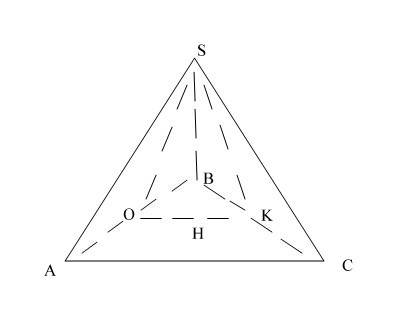
Все ребра пирамиды равны 8.
Рассмотри треугольник АВС - равносторонний. Сечение проходит через середины сторон АВ и ВС, следовательно, ОК - средняя линия. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. ОК=4.
Рассмотрим треугольник BSA - равнобедренный. SO является медианой, высотой и биссектрисой.
Рассмотрим треугольник SOA - прямоугольный.
SO^2 = SA^2 - OA^2
SO=корень из 48
Рассмотрим треугольник SHO - прямоугольный.
SH^2 = SO^2 - OH^2
SH=корень из 44
S сеч = 1/2 * OK * SH = 2 корня из 44.
Объяснение:
1) a^2 + b^2 = c^2
Где а и b - это катеты прямоугольного треугольника, а с - гипотенуза.
с^2 = 3^2 + 7^2 = 9 +49 = 58
С = √58
2) 9^2 = b^2 + 4^2
b^2 = 9^2 - 4^2 = (9-4)(9+4) = 5 × 13 = 65
b = √65
3) D1 ^2 + D2 ^2 = 4a ^2
10 ^2 + 24 ^2 = 4a ^2
100 + 576 = 4a ^2
4a ^2 =676
a^2 = 169
Так как длина стороны должна быть числом положительным, то а=13
4) Как и в пункте №1 a^2 + b^2 = c^2 где гипотенуза прямоугольного треугольника является диагональю прямоугольника.
d^2 = 8^2 + 5^2 = 64 + 25 = 89
d = √89
5) На фото (в приложении)
S = 3√7
6) так же в приложении
h = 8