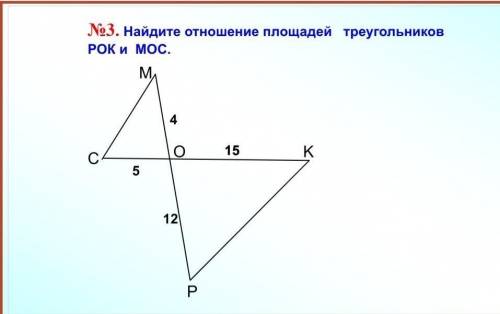
Объяснение:
Можно еще проще:
1) Углы MOC и KOP равны (вертикальные).
2) S треугольника CMO=0.5*MO*CO*sinO=0.5*4*5sinO=10sinO
S треугольника OPK=0.5*OK*OP*sinO=0.5*15*12*sinO=90sinO
3) А значит отношение площадей - равно 90/10=9
1. 1) любые две точки всегда принадлежат прямой, т.к. через две различные точки можно провести одну и только одну прямую, а уж если две точки сливаются в одну - и тем более.
2) Любые три точки всегда лежат в одной плоскости, поскольку через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну, если же они находятся на одной прямой, то через них можно провести бесчисленное множество плоскостей, и выбрать одну, в которой лежат эти точки, а вот четвертую точку можно положить в плоскость, или "подвесить" в пространство, т.е. ответ на этот вопрос НЕТ. т.к. не всегда.
2. Если две различные плоскости имеют общую точку, то они пересекаются по ПРЯМОЙ, проходящей через эту точку. т.е. общих не только одна, а все, лежащие на прямой. ответ НЕТ.
3. Нет. Т.к. не всегда третью можно положить на ту же плоскость, даже если они все три пересекаются. Нарисуйте две пересекающиеся прямые, они всегда лежат в одной плоскости и проведите прямую, которая проходит через точку пересечения, перпендикулярно двум данным, т.е. плоскости. Ясно, что эта третья прямая не лежит в данной плоскости.
4.1) Прямая, имеющая только одну общую точку с окружностью, так и называется касательной к окружности, если речь о плоскости.
2) если речь о пространстве, то та прямая, которая перпендикулярна радиусу, будет касательной, если же прямаЯ, проходящая через эту единственную точку, не перпендикулярна радиусу, касательной к окружности она не будет. Поэтому здесь ответ нет.
1. 1) любые две точки всегда принадлежат прямой, т.к. через две различные точки можно провести одну и только одну прямую, а уж если две точки сливаются в одну - и тем более.
2) Любые три точки всегда лежат в одной плоскости, поскольку через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну, если же они находятся на одной прямой, то через них можно провести бесчисленное множество плоскостей, и выбрать одну, в которой лежат эти точки, а вот четвертую точку можно положить в плоскость, или "подвесить" в пространство, т.е. ответ на этот вопрос НЕТ. т.к. не всегда.
2. Если две различные плоскости имеют общую точку, то они пересекаются по ПРЯМОЙ, проходящей через эту точку. т.е. общих не только одна, а все, лежащие на прямой. ответ НЕТ.
3. Нет. Т.к. не всегда третью можно положить на ту же плоскость, даже если они все три пересекаются. Нарисуйте две пересекающиеся прямые, они всегда лежат в одной плоскости и проведите прямую, которая проходит через точку пересечения, перпендикулярно двум данным, т.е. плоскости. Ясно, что эта третья прямая не лежит в данной плоскости.
4.1) Прямая, имеющая только одну общую точку с окружностью, так и называется касательной к окружности, если речь о плоскости.
2) если речь о пространстве, то та прямая, которая перпендикулярна радиусу, будет касательной, если же прямаЯ, проходящая через эту единственную точку, не перпендикулярна радиусу, касательной к окружности она не будет. Поэтому здесь ответ нет.
Докажем сначала, что они подобные. Углы MOC и KOP вертикальные, следственно, они равны.
KO/CO=PO/MO=3 они пропорциональны, значит по признаку подобия, один угол и две прилежащие пропорциональные стороны.
Коэффициент k=3.
Отношение площадей равен квадрату коэффициента.
Отношение 9:1