Общее уравнение окружности имеет вид:
(x – a)²+(y – b)²=r²
где a и b – координаты х и у центра окружности соответственно.
Получим:
(х–3)²+(у–2)²=r²
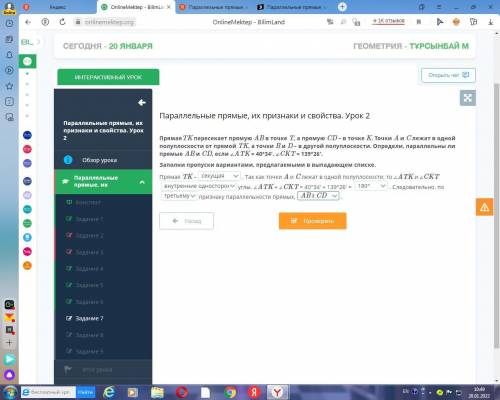
Найдем r. Радиус – это расстояние от центра (пусть это будет точка О) до любой точки на окружности (пусть данная в условии точка будет точка А)
Тогда АО=r; AO²=r².
Проведём из точки А прямую паралельную оси Оу, проведём прямую из точки О паралельную оси Ох. Точка пересечения будет точка В.
Так как кординатные оси перпендикулярны, тоесть образуют угол в 90°, то угол АВО так же будет равен 90°. Тогда ∆АВО – прямоугольный.
В прямоугольном треугольнике АВО по теореме Пифагора:
АО²=АВ²+ВО²
АО²=(5–2)²+(7–3)²
АО²=9+16
АО²=25
Тогда получим:
(х–3)²+(у–2)²=25
ответ: (х–3)²+(у–2)²=25
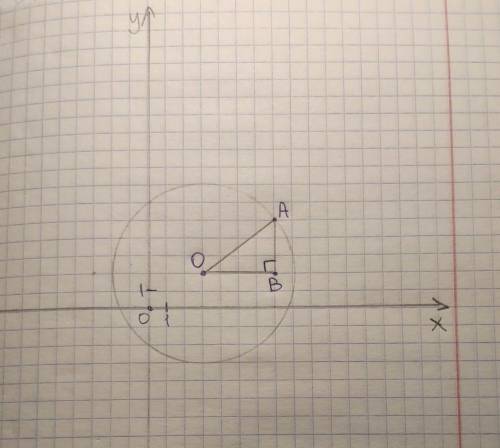
ответ:секущая , внутренние односторонние , 180, третьему, АВIICD
Объяснение: