
Объяснение:
2) ∠MNP + ∠N = 180° - как смежные
∠N = 180° - ∠MNP = 180° - 135° = 45°
ΔMNK - равнобедренный, значит ∠M = ∠N = 45°
ответ: 45°
3) ΔАВС прямоугольный, значит АС и ВС - катеты, АВ - гипотенуза
∠А = 30°, а катет, лежащий напротив угла в 30° равен половине гипотенузы ⇒ ВС = 12 / 2 = 6 см
АС² + ВС² = АВ² (по теореме Пифагора) ⇒ АС² = АВ² - ВС²
АС² = 12² - 6² = 144 - 36 = 108
АС = √108 ≈ 10 см
ответ: 10 см
4) ΔАВС прямоугольный, значит АС и ВС - катеты, АВ - гипотенуза
∠В = 30°, а катет, лежащий напротив угла в 30° равен половине гипотенузы ⇒ АВ = 7.5 * 2 = 15 см
ответ: 15 см
5)∠А = ∠МАN - как вертикальные ⇒ ∠А = 27°
Сумма углов треугольника равна 180°
ΔАВС = 180° = ∠А + ∠В + ∠С
∠А = 180° - 90° - 27° = 63°
ответ: 63°
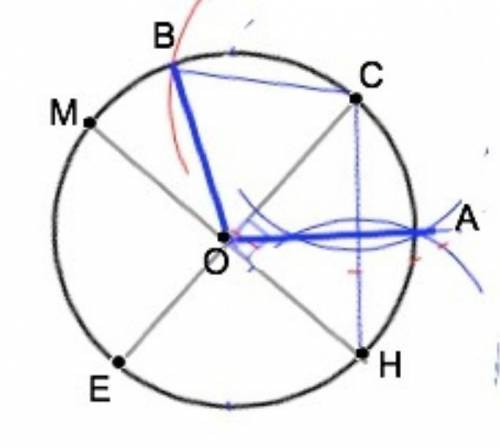
Чертим окружность с центром О.
Через О проводим диаметр МН и перпендикулярно к нему радиус ОС, (как строить срединный перпендикуляр - ниже) .
Соединим С и Н отрезком и разделим его пополам:
Для этого из т.С и Н чертим полуокружности (можно тем же радиусом, что и первая) так, чтобы они пересеклись по обе стороны от СН.
Точки пересечения полуокружностей соединим прямой, которая пройдет через О, т.к. ∆ НОС - равнобедренный, а срединный перпендикуляр равнобедренного треугольника - биссектриса. Точку пересечения с окружностью обозначим А. Угол СОА=45°.
Ставим ножку циркуля в т. С ( или А - не имеет значения) и раствором циркуля, равным радиусу первой окружности, делаем на ней насечку. Отмечаем т.В. ∆ ВОС - правильный, так как ВО=СО=ВС=R. ⇒
Угол ВОС=60°.
Угол ВОА=60°+45°=105° Построение завершено.
1) Рассмотрим ΔАВС
2) S квадрата = S треугольника = 324
3) S квадрата =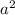
ответ: сторона квадрата = 8