Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.
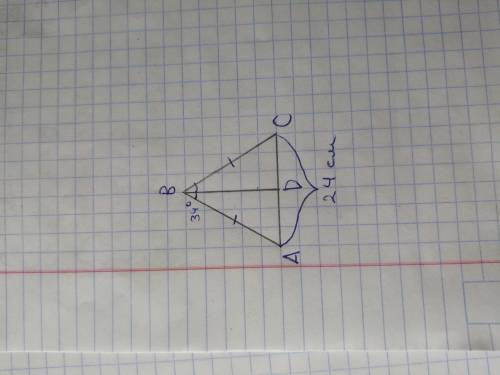
Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.

Пусть х градусов <ВDE, тогда
<СDE=(x-10) градусов
<ВDC=90 градусов, т. к СD перпендиклярен АВ.
Х+Х-10=90
2Х=90+10
2Х=100
Х=50 градусов
<BDE=50 градусов
ответ : <ВDE=50 градусов