
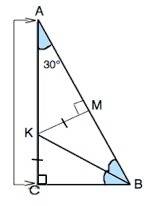
Обозначим данный треугольник АВС, ∠С=90°, ∠А=30°, ВК- биссектриса ∠АВС, КМ⊥АВ.
Сумма острых углов прямоугольного треугольника равна 90°.
∠САВ=30°, ∠АВС=60°.
Биссектриса делит угол пополам, ⇒∠КВС=∠КВМ=30°
Прямоугольные ∆ КВС=∆ КВМ по острому углу и общей гипотенузу. ⇒
КС=КМ.
В ∆ АКМ катет КМ противолежит углу 30° и равен половине гипотенузы АК (свойство).
Примем КМ=а
Тогда АК=2а
Так как КС=КМ, то АС=3а
3а=18, а=6 см.
КС=а=6 см, КА=18-6=12 см
* * *
Решить задачу можно разными Например, по т. Пифагора найти АВ и ВС и применить и свойство биссектрисы, которая делит противоположную углу сторону в отношении прилежащих сторон. Можно воспользоваться функциями острых углов, - это зависит от темы, которую в настоящее время проходите, но данное решение самое простое.
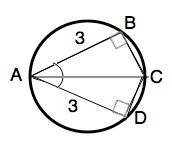
Окружность проведена через А, следовательно, А лежит на окружности.
АВ и АD - равные стороны вписанного угла ВАD, поэтому его биссектриса АС проходит через центр окружности и является её диаметром .
∠АВС=∠АDC=90°- опираются на диаметр.
Треугольники АВС и АBD равны по катету и гипотенузе, поэтому площадь каждого равна половине площади четырехугольника АВСD - равна 1,5√3
Площадь прямоугольного треугольника равна половине произведения его катетов.
S ∆ АВС=АВ•BC:2
BC=2S:AB=3√3):3=√3
ВС:АВ=tg∠ВАС
tg∠BAC=√3):3=1:√3. Это тангенс угла 30°.
Тогда, так как ∠ВАС=∠DAC, угол ВАD=60°
* * *
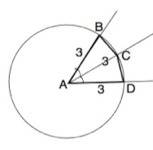
Если А - центр окружности, результат будет тот же, но решение немного другим Тогда АВ=АС=AD=R
AB+AD=6 AB=AD=AC=6:2=3⇒ R=3
АС - биссектриса. ∠ВАС=∠DAC⇒∆ ABC=∆ ADC по 1 признаку равенства треугольников.
S∆ ВАС=S∆DAC= S ABCD:2
sin BAC=2•SBAC:AB²⇒
sin BAC=3√3):9=√3:3=1/√3 - это синус 30°
Тогда, т.к. АС биссектриса, угол ВАD=60° Это ответ.
----------
1)угол АСВ=44 по теории о парал.прямых
смежный угол ЕDA, ЕDС = 78, а по Т. о смеж.углах известно, что
сумма смеж.углов равна 180⇒
АDС = 180 - 78 = 102
теперь нам известно 2 угла из треугольника АDС (сумма углов равна 180), то есть, 180 - 44 - 102 = 34.
угол АСD = 34
но тут, чтобы узнать угол АСВ нужно 180-102 - 34= 44(так мы нашли его)
2) теперь можно найти угол ВАС:
тут опять же смеж.углы, то есть, 180-44=136
а по условию известно что секущая делит угол КАС пополам, ⇒ 136:2=68
3)теперь в треугольнике АВС нам известно 2угла
1угол= 68
2угол = 44
а сумма всех углов в треугольнике равна 180
и так мы можем узнать угол АВС ⇒
180-68-44=68
угол АВС = 68
угол АСВ=44
угол ВАС=68