ответ: TS=4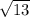
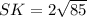
ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
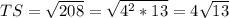 (см),
(см),
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
2RT*RS *соs ∠R =RS²;
RT*RS соs ∠R =RS²/2
В ΔRKS : RK=RT/2.
По теореме косинусов
SK²=RK²+RS²-2RK*RS*cos∠R=(RT/2)²+RS²-2(RT/2)*RS* соs ∠R=
=TR²/4+RS²- RT*RS* соs ∠R =TR²/4+RS² - RS²/2=
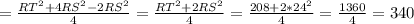
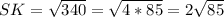
DF = 11,7 см.
Объяснение:
Задание: Дано два треугольника, ABC и DEF.
AB = 7 см, BC = 8 см, AC = 9 см, DE = 10,4 см, EF = 9,1 см.
Найти длину DF, если известно, что треугольники подобны.
У подобных треугольников соответствующие стороны пропорциональны друг другу.
Найдем, какие стороны пропорциональны и с каким коэффициентом.
k = 7 : 9,1 = 8 : 10,4 = 10 : 13
k = AB : EF = BC : DE = AC : DF
Осталось разделить AC на этот коэффициент и получить DF
DF = AC : k = 9 : (10/13) = 9*13/10 = 117/10 = 11,7 см