а) Пусть катет равен х см, тогда по теореме Пифагора :
х² + х² = 8²
2х² = 64
х² = 32
х = √32 = 4√2
Площадь прямоугольного треугольника можно найти по формуле S = 0.5 * a * b (а и b это катеты)
S = 0.5 * 4√2 *4√2 = 4*4 = 16 (см²)
б) 1,4дм = 14 см
Пусть катет будет равен х см, тогда по теореме Пифагора :
х² + х² = 14²
2х² = 196
х² = 98
х = √98 =7√2 см
S = 0.5*7√2 *7√2 = 7*7 = 49см² = 0.49 дм²
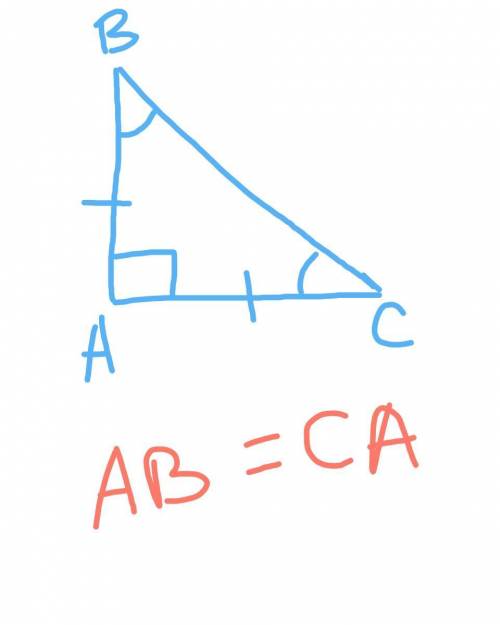
в)пусть катет также будет равен х м , по теореме Пифагора :
х² + х² = с²
2х² = с²
х² = с²/2
х = с/√2
S = 0.5 * (c/√2) * (c/√2) = c²/4 (м²)
шестигранник разделим не 6 треугольников, причем 1.5 см - это будет диаметр вписанной окружности.Тогда радиус вписанной окружности = 0,75 см.
Рассмотрим один такой треугольник.
Угол при центре окружности равен 360/6=60 град, значит треугольник равнобедренный, тогда углы при основании = (180-60)/2=60град - значит треугольник равносторонний, тогда радиус описанной окружности - высота этого треугольника и биссектриса для угла при центре окружности, тогда углы в таком треугольнике будут 30, 60, 90, значит
Пусть гипотенуза - 2х, тогда один катет, напротив угла60=0,75, а второй катет напротив угла 30=половина гипотенузы=х , тогда
по т Пиф 
Тогда площадь шестиугольника=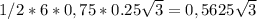
см квадратных
вот и всё
9,65
Объяснение:
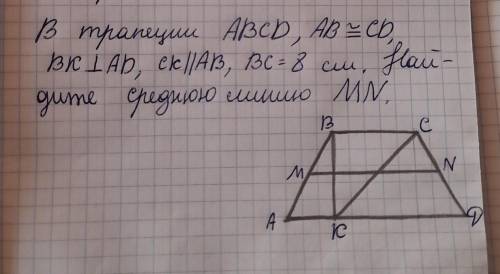
l=ab/2 (формула для средней линии трапеции)
a,b - основания; l - средняя линия.
1) AK = 8, т.к. нам дано, что ВСАК - п параллелограмм.
2) на мой взгляд, тут нужно провести ещё одну диагональ из , а также опустить высоту CH. Мы получим квадрат CBKH и два одинаковых треугольника. АК и HD =8.
Также между этими треугольникАми образовался ещё один равнобедренный треугольник, назовем его KMH, чтобы найти нижнее основание трапеции, осталось найти отрезок KH.
3) Его мы можем найти из прямоугольного треугольника CKH. Для этого применим теорему Пифагора. Сумма квадратов катетов равна квадрату гипотенузы:
8²+8²= 64+64=128
Итак, сложим все части:
8+8+11,3=27,3
4) теперь можно найти среднюю линию: