Определим величину угла СВА.
Угол СВА = 180 – АСВ – ВАС = 180 – 35 – 75 = 700.
Так как ВД, по условию, биссектриса угла АВС, то угол СВД = АВД = АВС / 2 = 70 / 2 = 350.
В треугольнике ВСД, угла при основании ВС равны 350, следовательно треугольник ВДС равнобедренный, а ДВ = ДС, что и требовалось доказать.
2).
Рассмотрим треугольники ВСД и АВД. В треугольнике АВД угол АДВ = 180 – 30 – 75 = 750.
Треугольники ВСД и АВД равнобедренные с одинаковыми сторонами. ВД = СД = ВД = ВА.
Сравним основания ВС и АД. Основание СД лежит против угла 750, а основание АД против угла 300, следовательно ВС > АД.
ответ: ВС > АД.

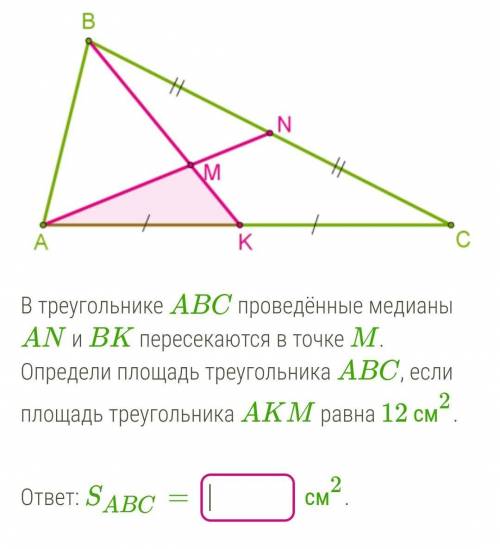
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
следовательно ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты), следовательно:
Samk/Sabm=1/2 следовательно:
12/Sabm=1/2 следовательно:
24=Sabm.
Sabk=24см²+12см²=36см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=36*2=72см².
ответ: 72см²