Главная тема тютчевской поэзии – человек и мир, человек и Природа. Исследователи Тютчева говорят о поэте как «певце природы» и видят своеобразие его творчества в том, что «у одного Тютчева философское восприятие природы составляет в такой сильнейшей степени самую основу видения мира». Более того, как отмечает Б.Я. Бухштаб, «в русской литературе до Тютчева не было автора, в поэзии которого природа играла бы такую роль. Природа входит в поэзию Тютчева как основной объект художественных переживаний».
Мир в представлении Тютчева – это единое целое, но не застывшее в «торжественном покое», а вечно меняющееся и в то же время подверженное вечному повторению во всех своих изменениях. Исследователи говорят о «неслучайности» «пристрастия поэта к переходным явлениям в природе, ко всему, что несет с собой изменение, что в конечном итоге связано с понятием «движения».
Своеобразие тютчевских пейзажей отчетливо видно в стихотворении, созданном в родовом имении Овстуг в 1846 г.:
Тихой ночью, поздним летом,
Как на небе звезды рдеют,
Как под сумрачным их свет
Объяснение:
Объяснение:
Площадь трапеции равна произведению полусуммы ее оснований ( средней линии) на высоту.
S= ВН*(АД+ВС):2
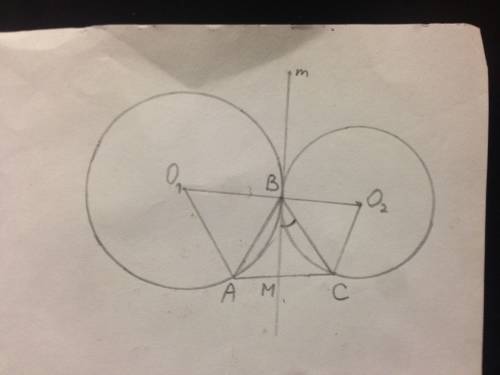
Сделаем рисунок к задаче.
Обозначим вершины трапеции АВСД.
Меньшее основание обозначим ВС, большее АД
Стороны трапеции делятся каждая на отрезки от вершин ( точки вне окружности) до точки касания.
Отрезки касательных, проведенные из одной точки, равны.
Меньшее основание от вершин тупых углов до точки касания по 8 см, и равно 8+8=16см.
Большее основание от вершин острых углов равно 18+18=36 см
Полусумма оснований равна
(36+16):2=26 см
Теперь нужно найти высоту трапеции.
Опустим из вершины тупого угла высоту ВН на АД.
Расстояние от угла большего основания равнобедренной трапеции до основания высоты, опущенной из вершины меньшего основания, равно полуразности оснований.
АН=(36-16):2=10 см
Высоту ВН найдем по теорем Пифагора:
ВН² =АВ²-АН²
ВН² =(8+18)²-10²=
ВН=24 см
S= ВН ∙(АД+ВС):2
S= 24 ∙26= 624 см²