1. Сторона треугольника равна 6 см, а высота, проведенная к ней, в два раза больше стороны.
Объяснение: Сторона = 6 см
Высота 6*2 = 12 (В два раза больше)
Площадь треугольника = Произведению основания на высоту и делённое на два.
Получаем: (6*12)/2 = 36
2. Катеты прямоугольного треугольника равны 3 см и 4 см. Найдите гипотенузу и площадь треугольника.
Объяснение: c²=a²+b²
c²=9+16
c²=25
c=5 см.
Sтреугольника = (3*4)/2 = 6 см.
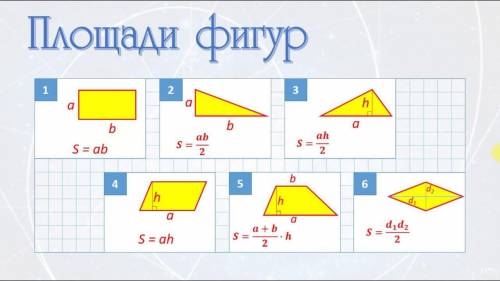
5. Выписать формулы для нахождения площади
прямоугольника, треугольника , параллелограмма, ромба,
квадрата, трапеции.
Объяснение:
А - (см) - катет 1, против известного угла
Б - (см) - катет 2, соприкасается с известным углом
С - (см) - гипотенуза
1) Определить значение тангенса угла ТАН (известный угол)
2) Определить длину неизвестного катета через тангенс ТАН (известный угол) = А / Б
- если известен катет (А) лежащий против известного угла, то находишь катет Б
Б = А / ТАН (известный угол)
- если известен прилежащий катет (Б) к известному углу, то находишь катет А
А = Б * ТАН (известный угол)
3) Определить по теореме Пифагора длину гипотенузы (С) - С^2 = А^2 + Б^2,
откуда С = корень квадратный из ( А^2 + Б^2)
4) Определить ПЕРИМЕТР = А+Б+С (см)
5) Определить ПЛОЩАДЬ треугольника равную половине произведения его катетов. т. е. S = ( 1/2 х А х Б ) (кв. см)