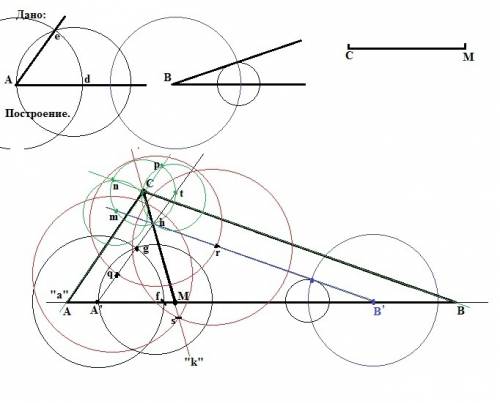
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Построение: 1) На произвольной прямой"а" обозначаем точку А', и строим с циркуля и линейки первый данный угол. Для этого с центром в вершине А данного угла проводим дугу, получая на сторонах угла точки "d" и "e" и этим же радиусом проводим дугу с центром в точке А' на прямой "а", получая точку "f" на прямой "а". Затем с циркуля радиусом = "de" из точки "f" проводим дугу и на пересечении двух дуг получаем точку "g". Проводим луч А'g. Таким образом один угол построили.
2) Из произвольной точки В' на прямой "а" точно так же строим второй данный нам угол.
3) В точке пересечения сторон двух построенных углов получили вершину "h" третьего угла. Строим биссектрису третьего угла. Для этого из точки "h" произвольным радиусом проводим окружность и получаем на сторонах угла точки "r" и "q". Из этих точек как из центров проводим окружности, получая в точке их пересечения точку "s". Через вершину "h" и точку "s" проводим прямую "k". Это и будет биссектриса угла, которая пересекает прямую "а" в точке М.
4) Откладываем на биссектрисе "k" от точки М отрезок МС, равный данному. Точка С - вершина искомого треугольника.
5) Проводим через точку С прямые, параллельные прямым Ah и Bh и в точках пересечения этих прямых с прямой "а" получаем вершины А и В искомого треугольника. Для этого:
a. Проводим окружность с центром в точке C радиусом Ch'.
b. На прямой "A'h" в месте пересечения с этой окружностью ставим точку t.
c. Проводим вторую окружность с центром в точке t радиусом Ch.
В месте пересечения этих окружностей ставим точку р.
d. Проводим третью окружность с центром в точке m радиусом Ch.
Получаем точку n на пересечении этой и первой окружностей.
e. Через точки m и h, t и h проводим прямые. Это и будут прямые АС и ВС параллельные прямым A'h и B'h.
Треугольник АВС построен.
Доказательство: углы А и В треугольника АВС равны данным, так как они являются соответственными углами при параллельных прямых АС и A'h и BC и B'h и секущей "а". Биссектриса третьего угла C равна данному отрезку СМ.
Відповідь:
65°
Пояснення:
180°-115°=65°