Zmeura1204
Объяснение:
1)
Дано:
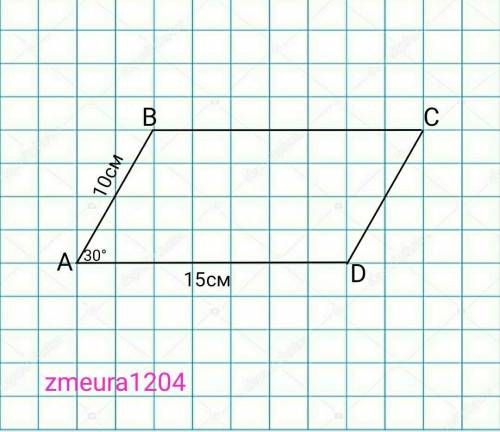
АВСD-параллелограм
AB=10см
AD=15см
<А=30°
S=?
_______
Решение
S=AB*AD*sin<A
sin<30°=1/2
S=1/2*10*15=75см²
ответ: 75см²
2)
Дано:
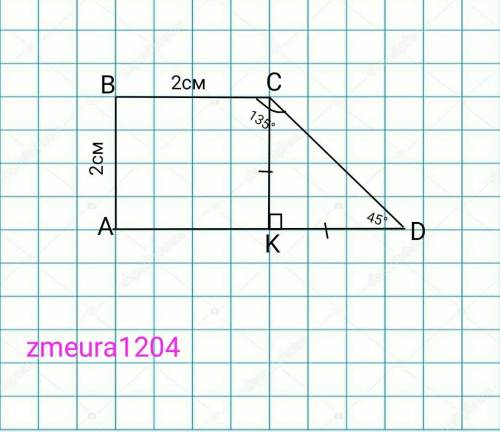
ABCD- трапеция
<ВАD=<ABC=90°
<BCD=135°
BC=2см
АВ=2см
S(ABCD)=?
______
Решение
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<CDK=180°-<BCD=180°-135°=45°
Проведём высоту СК.
∆CKD- прямоугольный равнобедренный треугольник (углы при основании равны. <СКD=90°; <CDK=45°; <KCD=90°-45°=45°)
CK=KD=AB=2см
АD=BC+KD=2+2=4см.
S(ABCD)=CK(BC+AD)/2=2(2+4)/2=6см²
ответ: 6см²
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5