ответ:
дана прямая а и точка м, не лежащая на ней.
проводим дугу с центром в точке м (черная), произвольного радиуса, большего расстояния от точки м до прямой.
получили две точки пересечения дуги и прямой а. обозначим их а и в.
теперь построим две окружности (красных), с центрами в данных точках, произвольного одинакового радиуса (большего половины отрезка ав).
точки пересечения этих окружностей назовем к и н.
проводим прямую кн.
кн - искомый перпендикуляр к прямой а.
доказательство:
если точка равноудалена от концов отрезка, значит она лежит на серединном перпендикуляре к отрезку.
ак = кв как равные радиусы, значит к лежит на серединном перпендикуляре к отрезку ав.
ан = нв как равные радиусы, значит н лежит на серединном перпендикуляре к отрезку ав.
кн - серединный перпендикуляр к отрезку ав.
ма = мв как равные радиусы черной окружности, значит и точка м лежит на прямой кн, т.е. перпендикуляр к прямой а проходит через точку м.
Решение задачи:
Доказательство строим на факте, что биссектриса AF делит угол BAD на два равных угла:
BAF = FAD
По правилу накрест лежащих углов при параллельных прямых AB и CD:
∠BAF = ∠ DFA.
Тогда углы FAD и DFA тоже равны, так как BAF = FAD. Значит, треугольник AFD – равнобедренный с основанием AF. Следовательно, AD = DF. По тем же причинам в треугольнике BCF BC = CF. В параллелограмме противоположные стороны равны – значит, BC = AD. Но тогда CF тоже равен AD, а значит, равен также FD. Если CF = FD, то F – середина CD.
Что и требовалось доказать.
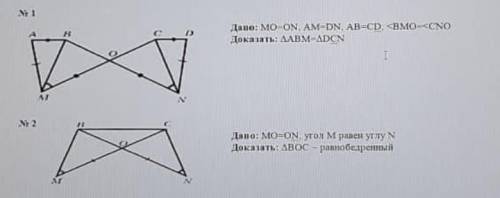
№1
Рассмотрим △MBO и △NCO, у которых: ∠BMO = ∠CNO, MO = NO (по условию) и ∠BOM = ∠CON как вертикальные углы при пересечении прямых BN и MC. Тогда △MBO = △NCO по 2 признаку равенства треугольников (по стороне и двум прилежащим к ней углам). Тогда из равенства треугольников получаем: MB = NC.
Рассмотрим треугольники △ABM и △DCN у которых AM = DN, AB = CD (по условию) и MB = NC. Тогда △ABM = △DCN по 3 признаку равенства треугольников (по трем сторонам), что и требовалось доказать.
№2
Рассмотрим △MBO и △NCO у которых: MO = ON, ∠M = ∠N,
∠BOM = ∠CON (как вертикальные углы при пересечении прямых BN, MC). Тогда △MBO = △NCO по 2 признаку равенства треугольников (по стороне и двум прилежащим к ней углам). Тогда из равенства треугольников получаем: BO = CO.
Рассмотрим △BOC,у которого BO = CO, тогда данный треугольник является равнобедренным по определению что и требовалось доказать.