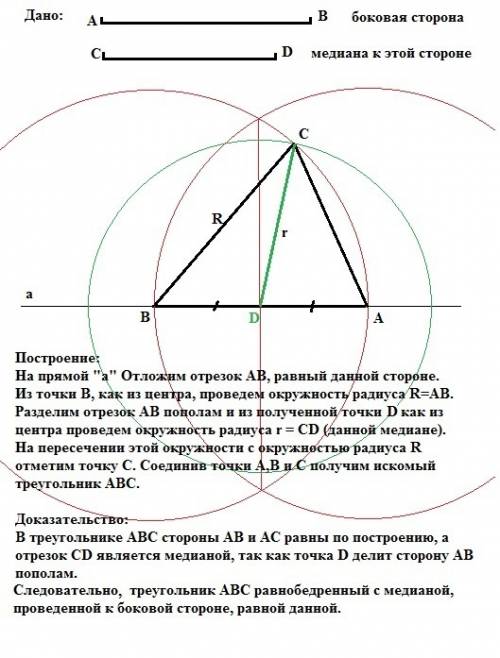
Построение:
На прямой "а" Отложим отрезок АВ, равный данной стороне. Из точки В, как из центра, проведем окружность радиуса R=AB. Разделим отрезок АВ пополм, отметим середину отрезка точкой D и из полученной точки D как из центра проведем окружность радиуса r = CD (равного данной медиане). На пересечении этой окружности с окружностью радиуса R отметим точку С. Соединив точки А,В и С получим искомый треугольник АВС.
Доказательство:
В треугольнике АВС стороны АВ и АС равны по построению, а отрезок CD является медианой, так как точка D делит сторону АВ пополам. Следовательно треугольник АВС равнобедренный с медианой, проведенной к боковой стороне, равной данной.
Дано:
ΔABC, ΔDEF
УголB=углуE=80°
уголF=70°
Объяснение:
1.
D+E+F=180°
D+80°+70°=180
D=180°-80°-70°
D=30°
2.
ΔABC подобен ΔDEF
(т.к. стороны ΔABC в 3 раза больше сторон ΔDEF, уголB=углуЕ)
значит:
уголE=углуВ=80°
уголС=углуF=70°
уголА=углуD=30°
3.
3DF=AC
3*9=27
AC=27
ответ: уголС=30°; АС=27см