Question

Отрезок AD - биссектриса треугольника АВС. Найдите: 1) отрезки BD и CD, если AB = 10 см, AC = 12 см, ВС= = 11 см; 2) сторону AC, если BD: DC = 4:9, AB = 16 см; 3) стороны AB и AC, если AB + AC = 32 см, BD: DC = = 5: 3.

Answer 1

Объяснение:

                   A

                   /|\

                /   |   \

             /      |      \

          /|\

      C           D         B

А) отрезки BD и CD, если AB = 10 см, AC = 12 см, ВС= = 11 см;

1)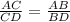 $\frac{AC}{CD}=\frac{AB}{BD}$ это по правилу (не помню как называлось)

BC=CD+BD=11

Легче будет представить, если CD=x, BD=y

1)$\frac{12}{x}=\frac{10}{y}$

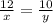
2)x+y=11

1) $10x=12y$

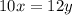
2)x=11-y

подставим

10(11-y)=12y

110-10y=12y

22y=110

y=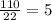$\frac{110}{22}=5$

x=11-5=6

СD=6 см

BD=5 см

2)сторону AC, если BD: DC = 4:9, AB = 16 см;

тоже используем эту схему

Пусть BD=4x, DC=9x

Тогда из того правила

$\frac{AC}{9x}=\frac{16}{4x}=AC=\frac{9x*16}{4x}= 36$ см

3) стороны AB и AC, если AB + AC = 32 см, BD: DC = = 5: 3.

Пусть AB=x, AC=y, тогда

$x+y=32\\\frac{x}{5} =\frac{y}{3} \\3x=5y\\x=32-y\\3(32-y)=5y\\96-3y=5y\\8y=96\\y=12\\x=32-12=20$

AB=20 см

AC= 12 см